Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Ta có góc SMH=90°; góc SNH=90°( góc nội tiếp chắn 1/2 đường tròn)
xét tứ giác SMHN có
góc SMH+ SNH=90°+90°=180°
suy ra SMHN nội tiếp
b, ta có góc SMN+NMB=90°
góc NBA+NAB=90°
mà góc NMB=NAB (góc nội tiếp chắn cung NB)
suy ra góc SMN = NBA
xét hai tam giác SMN và SBA có
góc S Chung
góc SMN=SBA (cmt)
suy ra hai tam giác đó đồng dạng
suy ra SM/SN=SB/SA
suy ra SM.SA=SN.SB(đpcm)
c,vì góc MON=70° suy ra cung MN=70°(góc ở tâm)
ta có cung AB=180°
mà góc ASB là góc ngoài chắn cung nhỏ MN và cung AB
suy ra góc ASB=(180-70)/2=55°
a)
ta có SA= SB(t/c tiếp tuyến cắt nhau)
nên tam giác SAB cân ở S
do đó SO vừa là phân giác vừa là đường cao nên SO vuông góc AB
I là trung điểm của MN nên OI vuông góc MN
do đó góc SHE=SIE = 90 độ
hai điểm H và I cùng nhìn đoạn SE dưới 1 góc vuông nên tứ giác IHSE nội tiếp
b) SOI đồng dạng với EOH vì có O chung
$\widehat{SHE}=\widehat{SIE}$ =90 độ chứng minh trên
suy ra $\dfrac{OI}{OH}$ = $\dfrac{OS}{OE}$
mà OH.OS = OB^2 = R^2(hệ thức lượng trong tam giác vuông SOB
nên OI.OE=R^2 (DPCM)
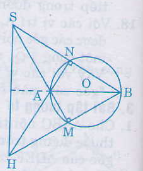
BM ⊥ SA ( =
vì là góc nội tiếp chắn nửa đường tròn).
Tương tự, có: AN ⊥ SB
Như vậy BM và AN là hai đường cao của tam giác SAB và H là trực tâm.
Suy ra SH ⊥ AB.
(Trong một tam giác ba đường cao đồng quy)
- Đề bài chắc chắn đúng chứ bạn? Mình tưởng phải có điều kiện đặc biệt ràng buộc C thì tam giác MAB mới cân được chứ nhỉ?
Xét (O) có
^AMB = ^ANB = 900 ( góc nt chắn nửa đường tròn )
nên AN ; BM lần lượt là đường cao
mà AN giao BN = H
=> H là trực tâm => SH là đường cao thứ 3
Vậy SH vuông AB
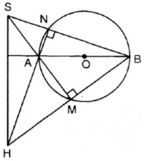
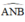là góc nội tiếp chắn nửa đường tròn ⇒ 
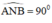⇒ AN ⊥ NB
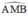là góc nội tiếp chắn nửa đường tròn ⇒ 
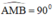⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.
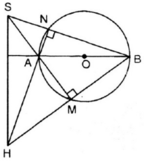
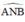là góc nội tiếp chắn nửa đường tròn ⇒ 
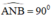⇒ AN ⊥ NB
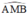là góc nội tiếp chắn nửa đường tròn ⇒ 
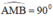⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)