Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét 2 \(\Delta\) \(ABD\) và \(EBD\) có:
\(AB=EB\left(gt\right)\)
\(\widehat{ABD}=\widehat{EBD}\) (vì \(BD\) là tia phân giác của \(\widehat{B}\))
Cạnh BD chung
=> \(\Delta ABD=\Delta EBD\left(c-g-c\right)\)
b) Theo câu a) ta có \(\Delta ABD=\Delta EBD.\)
=> \(AD=ED\) (2 cạnh tương ứng).
c) Theo câu a) ta có \(\Delta ABD=\Delta EBD.\)
=> \(\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^0\left(gt\right)\)
=> \(\widehat{BED}=90^0.\)
Câu d) thì mình nghĩ đã nhé.
Chúc bạn học tốt!

Bài 1 : a) b)*:\(5^x.\left(5^3\right)^2=625\)
b)*:\(5^x.\left(5^3\right)^2=625\)
\(5^x.5^6=5^4\)
\(5^x=5^4:5^6\)
\(5^x=5^{4-6}\)
\(5^x=5^{\left(-2\right)}\)
Mà \(x\in N\)
=>x\(\in\varnothing\)
Vậy x \(\in\varnothing\)
*:\(x^{10}=1^x\)
\(=>x^{10}=1\)
\(x^{10}=1^{10}\)
=> x = 1
Vậy x =1
Bài 2 : ( bài 2 này mk được học rồi nên mk mở lại sách nhá , chữ xấu mong bạn thông cảm , vì nó dài dòng nên mk mở lại sách cũ , ko muốn làm )


Bài 2:
\(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)
\(\Rightarrow\left(x-7\right)^{x+1}\left[1-\left(x-7\right)^{10}\right]=0\)
\(\Rightarrow\left(x-7\right)^{x+1}=0\) hoặc \(1-\left(x-7\right)^{10}=0\)
+) \(\left(x-7\right)^{x+1}=0\Rightarrow x-7=0\Rightarrow x=7\)
+) \(1-\left(x-7\right)^{10}=0\)
\(\Rightarrow\left(x-7\right)^{10}=1\)
\(\Rightarrow x-7=\pm1\)
+) \(x-7=1\Rightarrow x=8\)
+) \(x-7=-1\Rightarrow x=6\)
Vậy \(x\in\left\{7;8;6\right\}\)
Bài 6:
Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{2x+1}{5}=\frac{3y-2}{7}=\frac{2x+1+3y-2}{5+7}=\frac{2x+3y-1}{12}=\frac{2x+3y-1}{6x}\)
\(\Rightarrow6x=12\)
\(\Rightarrow x=2\)
Vậy x = 2

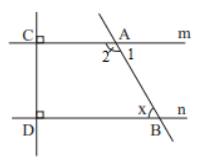
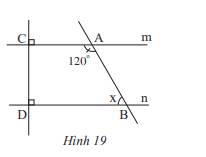
a) Vì m và n cùng vuông góc với CD nên m // n
b) Ta có: \(\widehat {{A_2}} + \widehat {{A_1}} = 180^\circ \Rightarrow 120^\circ + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - 120^\circ = 60^\circ \)
Vì m // n nên \(\widehat {{A_1}} = \widehat {ABD}\) ( 2 góc so le trong) nên \(\widehat {ABD}\) = 60\(^\circ \)
Vậy x = 60\(^\circ \)

Bài 1:
a, Xét \(\Delta\)ABM và \(\Delta\) CDM có:
MA = MC (gt)
MB = MD (gt)
\(\widehat{M_1}\) = \(\widehat{M_2}\) (đối đỉnh)
Vậy \(\Delta\)ABM = \(\Delta\)CDM (c-g-c)
b, Ta có: \(\widehat{B1}\) = \(\widehat{D}\) (Vì \(\Delta\)ABM = \(\Delta\)CDM )
Mà hai góc này ở vị trí sole trong
=> AB // CD
c, Ta có:
\(\Delta\)ABM = \(\Delta\)CDM (c.m.t)
=> AB = CD (2.c.t.ư)
Mà: CD = CN (gt)
=> AB = CN
Xét \(\Delta\)ABC và \(\Delta\) NCB có:
AB = CN ( c.m.t)
BC chung
\(\widehat{ABC}\) = \(\widehat{BCN}\)
=> \(\Delta\)ABC = \(\Delta\) NCB (c-g-c)
=> \(\widehat{B_2}\) = \(\widehat{C_1}\)
Mà hai góc này ở vị trí sole trong
=> BN = AC