
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

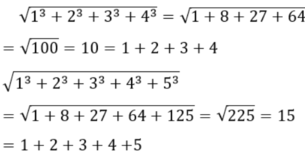

a) Đúng
b) \(\sqrt{1^3+2^3+3^3+4^3}=1+2+3+4\)
\(\sqrt{1^3+2^3+3^3+4^3+5^3=1+2+3+4+5}\)

Các đẳng thức trên luôn đúng:
Ta có công thức tổng quát
\(\sqrt{1^3+2^3+...+n^3}=1+2+..+n\)

THay x = -1/10 vào đa thức ta có
\(5\cdot-\frac{1}{10}+\frac{1}{2}=-\frac{1}{2}+\frac{1}{2}=0\)
Vậy -1/10 là nghiệm của pt
b, Thay x = 1/3 vào đa thức ta có;
\(3\cdot\frac{1}{3^2}+\frac{1}{3}-\frac{2}{3}=3\cdot\frac{1}{9}+\frac{1}{3}-\frac{2}{3}=\frac{2}{3}-\frac{2}{3}=0\)
Vậy x = 1/3 là nghiệm của pt.
Tương tự với x = -2/3 nha


câu 1:
1+x^3+y^2
câu 2
a, c=a+b=(\(x^2\)-2y+xy+1)+(\(x^2\)+y-x^2y^2-1)
=x^2-2y+xy+1+x^2+y-x^2y^2-1
= (x^2+x^2)+(-2y+y)+(1-1)+xy
= 2x^2-y+xy
b,c=b-a=(x^2-2y+xy+1)-(x^2 +y-x^2y^2-1)
= x^2-2y+xy+1-x^2-y+x^2y^2+1
=(x^2-x^2)+(-2y-y)+(1+1)+xy
=2x^2-3y+2+xy
cho mik nha
