Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{-49}{211}< \dfrac{13}{1999}\)vì số âm luôn luôn bé hơn số dương.

a: \(-\dfrac{49}{211}< 0\)
\(0< \dfrac{13}{1999}\)
Do đó: \(-\dfrac{49}{211}< \dfrac{13}{1999}\)
b: \(\dfrac{311}{256}>1\)
\(1>\dfrac{199}{203}\)
Do đó: \(\dfrac{311}{256}>\dfrac{199}{203}\)
c: \(\dfrac{99}{-98}< 0\)
\(0< \dfrac{33}{49}\)
Do đó: \(\dfrac{99}{-98}< \dfrac{33}{49}\)
d: \(\dfrac{105}{106}< 1\)
\(1< \dfrac{94}{93}\)
Do đó: \(\dfrac{105}{106}< \dfrac{94}{93}\)

\(\frac{18}{91}=\frac{558}{2821}\)
\(\frac{6}{31}=\frac{546}{2821}\)
=>\(\frac{18}{91}>\frac{6}{31}\)
Ta có : \(\frac{18}{91}< \frac{18}{90}\left(91>90\right)\)
\(\Rightarrow\frac{18}{91}< \frac{1}{5}\left(1\right)\)
\(\frac{6}{31}>\frac{6}{30}\left(31>30\right)\)
\(\Rightarrow\frac{6}{31}>\frac{1}{5}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\frac{18}{91}< \frac{1}{5}< \frac{6}{31}\)
\(\Rightarrow\frac{18}{91}< \frac{6}{31}\)
Chúc bạn học tốt !!!

a: 14/21=2/3=4/6
60/72=5/6
mà 4<5
nên 14/21<60/72
b: 38/133=2/7=16/56
129/344=3/8=21/56
mà 16<21
nên 38/133<129/344

a)\(\dfrac{1212}{2323}=\dfrac{1212:101}{2323:101}=\dfrac{12}{23}\)
b)\(\dfrac{-3435}{4141}< \dfrac{-3434}{4141}=\dfrac{-3434:101}{4141:101}\)
Nhận xét:
\(\dfrac{\overline{abab}}{\overline{cdcd}}=\dfrac{\overline{ab}}{\overline{cd}}\)

a: 17/200>17/314
b: 11/54=22/108<22/37
c: 141/893=3/19
159/901=3/17
mà 3/19<3/17
nên 141/893<159/901

Bài 1:
a) Ta có: \(13A=\dfrac{13^{16}+13}{13^{16}+1}=1+\dfrac{12}{13^{16}+1}\)
\(13B=\dfrac{13^{17}+13}{13^{17}+1}=1+\dfrac{12}{13^{17}+1}\)
Vì \(\dfrac{12}{13^{16}+1}>\dfrac{12}{13^{17}+1}\Rightarrow1+\dfrac{12}{13^{16}+1}>1+\dfrac{12}{13^{17}+1}\)
\(\Rightarrow13A>13B\)
\(\Rightarrow A>B\)
Vậy A > B
b) Ta có: \(1999C=\dfrac{1999^{2000}+1999}{1999^{2000}+1}=1+\dfrac{1998}{1999^{2000}+1}\)
\(1999D=\dfrac{1999^{1999}+1999}{1999^{1999}+1}=1+\dfrac{1998}{1999^{1999}+1}\)
\(\dfrac{1998}{1999^{2000}+1}< \dfrac{1998}{1999^{1999}+1}\Rightarrow1+\dfrac{1998}{1999^{2000}+1}< 1+\dfrac{1999}{1999^{1999}+1}\)
\(\Rightarrow1999C< 1999D\)
\(\Rightarrow C< D\)
Vậy C < D
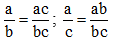
Ta có:
\(\dfrac{-49}{211}< 0;\dfrac{13}{1999}>0\)
⇒ \(\dfrac{-49}{211}< \dfrac{13}{1999}\)
-49/211<0<13/1999