Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(S< \dfrac{1}{2}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{31}+\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{32}\) \(=\dfrac{1}{2}+\dfrac{3}{11}+\dfrac{2}{31}+\dfrac{2}{32}\)
\(=\dfrac{4909}{5456}< \dfrac{9}{10}\)
\(\Rightarrow S< \dfrac{9}{10}\)
Vậy \(S< \dfrac{9}{10}\)

Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\\ \dfrac{1}{12}>\dfrac{1}{20}\\ ..........\\ \dfrac{1}{20}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\\ \Rightarrow S>\dfrac{10}{20}\\ \Rightarrow S>\dfrac{1}{2}\)

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

a, \(4\times\left(-\dfrac{1}{2}\right)^3-2\times\left(-\dfrac{1}{2}\right)^2+3\times\left(-\dfrac{1}{2}\right)+1\)
\(=\left(-\dfrac{1}{2}\right)\left[\left(4\times-\dfrac{1}{2}\right)-\left(2\times-\dfrac{1}{2}\right)+3\right]+1\)
\(=\left(-\dfrac{1}{2}\right)\left(-2+1+3\right)+1\)
\(=\left(-\dfrac{1}{2}\right)2+1\)
\(=-1+1\)
\(=0\)
@Trịnh Thị Thảo Nhi
a, 4×(−12)3−2×(−12)2+3×(−12)+14×(−12)3−2×(−12)2+3×(−12)+1
=(−12)[(4×−12)−(2×−12)+3]+1=(−12)[(4×−12)−(2×−12)+3]+1
=(−12)(−2+1+3)+1=(−12)(−2+1+3)+1
=(−12)2+1=(−12)2+1
=−1+1=−1+1
=0=0

Giải:
Đặt \(A=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{59}+\dfrac{1}{60}\)
Ta có:
\(A=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{59}+\dfrac{1}{60}\)
\(\Rightarrow A=\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)+\left(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}\right)\)
Nhận xét:
\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}< \dfrac{1}{30}+\dfrac{1}{30}+...+\dfrac{1}{30}=\dfrac{1}{3}\)
\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}< \dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}=\dfrac{1}{4}\)
\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}< \dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{1}{5}\)
\(\Rightarrow A< \dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}=\dfrac{47}{60}< \dfrac{48}{60}=\dfrac{4}{5}\)
\(\Rightarrow A< \dfrac{4}{5}\left(1\right)\)
Lại có:
\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}>\dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}=\dfrac{1}{4}\)
\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}>\dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{1}{5}\)
\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}>\dfrac{1}{60}+\dfrac{1}{60}+...+\dfrac{1}{60}=\dfrac{1}{6}\)
\(\Rightarrow A>\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=\dfrac{37}{60}>\dfrac{36}{60}=\dfrac{3}{5}\)
\(\Rightarrow A>\dfrac{3}{5}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{3}{5}< A< \dfrac{4}{5}\)
Vậy \(\dfrac{3}{5}< \dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{59}+\dfrac{1}{60}< \dfrac{4}{5}\) (Đpcm)
Đặt A=131+132+133+...+159+160A=131+132+133+...+159+160
Ta có:
A=131+132+133+...+159+160A=131+132+133+...+159+160
⇒A=(131+132+...+140)+(141+142+...+150)+(151+152+...+160)⇒A=(131+132+...+140)+(141+142+...+150)+(151+152+...+160)
Nhận xét:
131+132+...+140<130+130+...+130=13131+132+...+140<130+130+...+130=13
141+142+...+150<140+140+...+140=14141+142+...+150<140+140+...+140=14
151+152+...+160<150+150+...+150=15151+152+...+160<150+150+...+150=15
⇒A<13+14+15=4760<4860=45⇒A<13+14+15=4760<4860=45
⇒A<45(1)⇒A<45(1)
Lại có:
131+132+...+140>140+140+...+140=14131+132+...+140>140+140+...+140=14
141+142+...+150>150+150+...+150=15141+142+...+150>150+150+...+150=15
151+152+...+160>160+160+...+160=16151+152+...+160>160+160+...+160=16
⇒A>14+15+16=3760>3660=35⇒A>14+15+16=3760>3660=35
⇒A>35(2)⇒A>35(2)
Từ (1)(1) và (2)(2)
⇒35<A<45⇒35<A<45
Vậy 35<131+132+133+...+159+160<4535<131+132+133+...+159+160<45

Ta có:
\(C=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{60}\)
\(=\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)+\left(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}\right)\)
Nhận xét:
\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}< \dfrac{1}{30}+\dfrac{1}{30}+...+\dfrac{1}{30}\) \(=\dfrac{1}{3}\)
\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}< \dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}\) \(=\dfrac{1}{4}\)
\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}< \dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}\) \(=\dfrac{1}{5}\)
\(\Rightarrow C< \dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}=\dfrac{47}{60}< \dfrac{48}{60}=\dfrac{4}{5}\)
Vậy \(C< \dfrac{4}{5}\) (Đpcm)

Đặt: \(\left\{{}\begin{matrix}A=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{60}\\B=\dfrac{1}{1.2}+\dfrac{1}{3.4}+...+\dfrac{1}{59.60}\end{matrix}\right.\)
Ta có:
\(B=\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+...+\dfrac{1}{59.60}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{59}-\dfrac{1}{60}\)
\(=\left(1+\dfrac{1}{3}+...+\dfrac{1}{59}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{60}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{60}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{60}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{60}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{30}\right)\)
\(=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{60}\)
\(\Rightarrow B=A\)
Vậy \(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{60}=\dfrac{1}{1.2}+\dfrac{1}{3.4}+...+\dfrac{1}{59.60}\) (Đpcm)
Ta có:
\(\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+......+\dfrac{1}{59.60}\)
= \(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+......+\dfrac{1}{59}-\dfrac{1}{60}\)
= \(\left(1+\dfrac{1}{3}+\dfrac{1}{5}+....+\dfrac{1}{59}\right)+\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+....+\dfrac{1}{60}\right)\)
- \(2\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+....+\dfrac{1}{60}\right)\)
= \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{60}\right)\) - \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{30}\right)\)
=\(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{30}\right)\)+ \(\left(\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+....+\dfrac{1}{60}\right)\)
- \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{30}\right)\)
= \(\left(\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+....+\dfrac{1}{60}\right)\)
Vậy\(\left(\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+....+\dfrac{1}{60}\right)\)= \(\dfrac{1}{1.2}+\dfrac{1}{3.4}+....+\dfrac{1}{59.60}\)

Ta có: \(\dfrac{1}{11}>\dfrac{1}{20}\)
\(\dfrac{1}{12}>\dfrac{1}{20}\)
\(\dfrac{1}{13}>\dfrac{1}{20}\)
\(\dfrac{1}{14}>\dfrac{1}{20}\)
\(\dfrac{1}{15}>\dfrac{1}{20}\)
\(\dfrac{1}{16}>\dfrac{1}{20}\)
\(\dfrac{1}{17}>\dfrac{1}{20}\)
\(\dfrac{1}{18}>\dfrac{1}{20}\)
\(\dfrac{1}{19}>\dfrac{1}{20}\)
\(\dfrac{1}{20}=\dfrac{1}{20}\)
=> \(\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{20}>\dfrac{1}{20}.10\)
hay S > \(\dfrac{1}{2}\)
Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\) ( vì 1 > 0 , 0 < 11 < 20 )
\(\dfrac{1}{12}>\dfrac{1}{20}\) ( vì 1 > 0 , 0 < 12 < 20 )
...
\(\dfrac{1}{20}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\)( 10 số hạng )
\(\Rightarrow S>\dfrac{1}{20}.10\Rightarrow S>\dfrac{10}{20}\Rightarrow S>\dfrac{1}{2}\)
Vậy ...
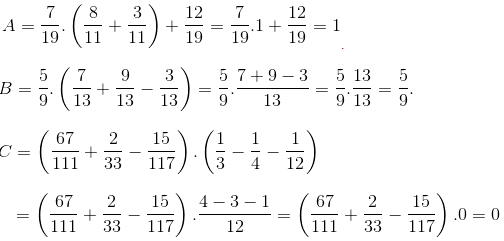
bn dựa vào câu trả lời của Quách Thùy Dung trong câu hỏi của The Dack Knight mà làm


giải chi tiết hơn