So sánh A = 7 + 15 và 7 A. A

Khách

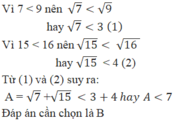
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

11 tháng 10 2018

So sánh A = 7 + 15 và 7

A. A > 7

B. A < 7

C. A = 7

D. A ≥ 7

#Toán lớp 7

Cao Minh Tâm

11 tháng 10 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Nguyễn Hồng Thanh

27 tháng 7 2017 - olm

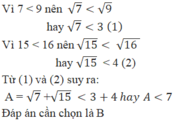
So sánh\(A=\frac{2^{2006}+7}{2^{2004}+7}\)và\(B=\frac{2^{2003}+1}{2^{2001}+1}\)

A A > B
B A = B
C A < B

#Toán lớp 7

༄NguyễnTrungNghĩa༄༂

27 tháng 7 2017

A < B nhá !!!

Đúng(0)

Nguyễn Hồng Thanh

27 tháng 7 2017

thanks nha

Đúng(0)

•๖ۣۜLү ²ƙ⁸ ( ๖ۣۜTεαм ๖ۣۜNɦâη ๖ۣۜMã ...

13 tháng 2 2020 - olm

Bài 2: Cho a, b,c là độ dài 3 cạnh của 1 tam giác và

M=\(\frac{7^a}{7^{b+c}}\) và N=\(\frac{7^a+2019}{7^{b+c}+2019}\)

so sánh M và N

#Toán lớp 7

Lâm Nguyệt Nhi

10 tháng 10 2017 - olm

\(\)SO SÁNH

a) 15 và \(\sqrt{235}\)

b) \(\sqrt{7}\)+ \(\sqrt{15}\)và 7

#Toán lớp 7

Despacito

10 tháng 10 2017

a) \(15=\sqrt{225}\)

\(\sqrt{235}=\sqrt{235}\)

vi \(225< 235\)nen \(\sqrt{225}< \sqrt{235}\)

vay \(15< \sqrt{235}\)

Đúng(0)

Akai Haruma

10 tháng 10 2017

Câu b)

Ta có \(\sqrt{7}< \sqrt{9}\Leftrightarrow\sqrt{7}< 3\)

\(\sqrt{15}< \sqrt{16}\Leftrightarrow\sqrt{15}< 4\)

Cộng theo vế: \(\sqrt{7}+\sqrt{15}< 3+4\) hay \(\sqrt{7}+\sqrt{15}< 7\)

Đúng(0)

hyun jung

10 tháng 1 2017 - olm

cho A=\(\frac{7^{2011}+1}{7^{2013}+1}\)và B=\(\frac{7^{2013}+1}{7^{2015}+1}\)HÃY SO SÁNH A VÀ B

#Toán lớp 7

Nguyễn Thi An Na

7 tháng 8 2019 - olm

Câu 1: Cho A.= \(\frac{7^{2018}+1}{7^{2019}+1}\)Và B=\(\frac{7^{2019}+1}{7^{2019}+1}\)

So sánh A và B

#Toán lớp 7

nguyễn tuấn thảo

7 tháng 8 2019

\(A=\frac{7^{2018}+1}{7^{2019}+1}\)

\(\Rightarrow7A=\frac{7^{2019}+7}{7^{2019}+1}=1+\frac{6}{7^{2019}+1}\)

\(B=\frac{7^{2019}+1}{7^{2020}+1}\)

\(\Rightarrow7B=\frac{7^{2020}+7}{7^{2020}+1}\)

\(\Rightarrow7B=1+\frac{6}{7^{2020}+1}\)

Vì 7 ^ 2019 < 7 ^ 2020 => 7 ^ 2019 + 1 < 7 ^ 2020 + 1

=> 6 / ( 7 ^ 2019 + 1 ) > 6 / ( 7 ^ 2020 + 1 )

=> 1 + 6 / ( 7 ^ 2019 + 1 ) > 1 + 6 / ( 7 ^ 2020 + 1 )

=> 7A > 7B

Vì A , B > 0

Nên A > B

Đúng(0)

Bùi Yến Nhi

7 tháng 8 2019

Vì \(7^{2018}< 7^{2019}\)nên \(7^{2018}+1< 7^{2019}+1\)

\(\Rightarrow\frac{7^{2018}+1}{7^{2019}+1}< \frac{7^{2019}+1}{7^{2019}+1}\)

Hay A < B

Chúc bạn học tốt ! Nguyễn Thi An Na

Đúng(0)

•๖ۣۜHυүềη ²ƙ⁷ ( ๖ۣۜTεαм ๖ۣۜBạ¢ɦ ๖ۣۜ...

14 tháng 2 2020 - olm

Cho a,b,c là độ dài của 3 cạnh của 1 tam giác và

M=\(\frac{\text{7^a}}{7^{b+c}}\) và N=\(\frac{\text{7^a +2019 }}{7^{b+c}+2019}\)

so sánh M và N ai nhanh tik nha thank you

#Toán lớp 7

shitbo

14 tháng 2 2020

\(a< b+c\text{ tính chất cạnh của t/giác:}\Rightarrow7^a< 7^{b+c}\Rightarrow\frac{7^a}{7^{b+c}}< 1\)

\(\text{Với: phân số }\frac{a}{b}\text{ có a;b nguyên dương bé hơn 1 thì:}\frac{a+n}{b+n}>\frac{a}{b}\left(\text{n nguyên dương}\right)\)

nên áp dụng cộng tử và mẫu của phân số M cho 2019 rồi ra N>M

Đúng(0)

Manaka Mukaido

8 tháng 10 2017 - olm

Cho \(A=7+7^2+7^3+7^4+...+7^{99}\)

a) So sánh A với \(\frac{7^{100}}{6}\)

b) Chứng minh rằng A chia hết cho 19

c) Tìm chữ số tận cùng của A

Mình cần gấp !

#Toán lớp 7

Lê Quang Phúc

8 tháng 10 2017

a) \(A=7+7^2+...+7^{99}\)

\(7A=7^2+7^3+...+7^{100}\)

\(7A-A=7^2+7^3+...+7^{100}-7-7^2-...-7^{99}\)

\(6A=7^{100}-7\)

\(A=\frac{7^{100}-7}{6}\)

Mà 7¹⁰⁰ > 7¹⁰⁰ - 7 => A < \(\frac{7^{100}}{6}\)

b) \(A=7+7^2+...+7^{99}\)

\(A=\left(7+7^2+7^3\right)+...+\left(7^{97}+7^{98}+7^{99}\right)\)

\(A=\left(7+7^2+7^3\right)+...+7^{96}.\left(7+7^2+7^3\right)\)

\(A=399+...+7^{96}.399\)

\(A=399.\left(1+...+7^{96}\right)⋮19\left(đpcm\right)\)

Đúng(0)

Manaka Mukaido

8 tháng 10 2017

Còn bn nào giải đc phần c không

Đúng(0)

Daily Yub

20 tháng 12 2019 - olm

So sánh

a,\(25^{15}\)và \(8^{10}.3^{30}\)

b\(\frac{4^{15}}{7^{30}}\)và \(\frac{8^{10}.3^{30}}{7^{30}.4^{15}}\)

#Toán lớp 7

Hoàng Thanh Huyền

20 tháng 12 2019

a) Ta có: \(25^{15}=\left(5^2\right)^{15}=5^{30}\)

\(8^{10}.3^{30}=\left(2^3\right)^{10}.3^{30}\)\(=2^{30}.3^{30}=6^{30}\)

Vì \(5^{30}< 6^{30}\)nên \(25^{15}< 8^{10}.3^{30}\)

b) Ta có: \(\frac{4^{15}}{7^{30}}=\frac{\left(2^2\right)^{15}}{7^{30}}=\frac{2^{30}}{7^{30}}\)

\(\frac{8^{10}.3^{30}}{7^{30}.4^{15}}=\frac{\left(2^3\right)^{10}.3^{30}}{7^{30}.\left(2^2\right)^{15}}=\frac{2^{30}.3^{30}}{7^{30}.2^{30}}=\frac{3^{30}}{7^{30}}\)

Vì \(2^{30}< 3^{30}\)nên \(\frac{2^{30}}{7^{30}}< \frac{3^{30}}{7^{30}}\)hay \(\frac{4^{15}}{7^{30}}< \frac{8^{10}.3^{30}}{7^{30}.4^{15}}\)

_Học tốt_

Đúng(1)

Hoàng Thảo Nhi

11 tháng 8 2017 - olm

Biết với \(a,b>0;a,b\in R\)

Thì \(a>b\Leftrightarrow\sqrt{a}>\sqrt{b}\)

\(a>b\Leftrightarrow a^2>b^2\)

Hãy so sánh

a) \(3\sqrt{2}\)và \(2\sqrt{3}\)

b) \(7\sqrt{6}\)và \(6\sqrt{7}\)

Giúp mik nha____mik cần gấp lắm-------ai nhanh mik tick cho ha >~<

#Toán lớp 7

uzumaki naruto

11 tháng 8 2017

a) Ta có: \(3\sqrt{2}=\sqrt{3^2.2}=\)\(\sqrt{18}\)

\(2\sqrt{3}=\sqrt{2^2.3}=\sqrt{12}\)

Do \(\sqrt{18}>\sqrt{12}=>3\sqrt{2}>2\sqrt{3}\)

b) tương tự trên

Đúng(0)

Phạm Quang Anh

11 tháng 8 2017

bạn thử bình phương 2 vế lên rùi so sánh

so sánh song thì kết luận

Đúng(0)

vuthaophuong

3 tháng 3 2021 - olm

a) \(A=\frac{3a-b}{2a+7}+\frac{3b-a}{2b-7}.\). Với b-a=7; a khác với \(\frac{-3}{5}\); b khác với \(\frac{3}{5}\)

b) so sánh: \(\sqrt{17}+\sqrt{26}+1\)và \(\sqrt{99}\)

#Toán lớp 7

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP