Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tanx=tan3pi/11
x=3pi/11+kpi
\(\frac{\pi}{4}< \frac{3\pi}{11}+k\pi< 2\pi\)
\(\frac{1}{4}< \frac{3}{11}+k< 2\)
\(\frac{1}{4}-\frac{3}{11}< k< 2-\frac{3}{11}\)
\(-\frac{1}{44}< k< \frac{19}{11}\)
\(\Rightarrow k=0;k=1\)
Vậy chọn B

\(tanx=tan\frac{3\pi}{11}\Rightarrow x=\frac{3\pi}{11}+k2\pi\)
Do \(\frac{\pi}{4}\le x\le2\pi\)
\(\Rightarrow\frac{\pi}{4}\le\frac{3\pi}{11}+k2\pi\le2\pi\)
\(\Rightarrow-\frac{1}{88}\le k\le\frac{19}{22}\)
Mà \(k\in Z\Rightarrow k=0\)
Vậy pt có đúng 1 nghiệm trên đoạn đã cho

\({\mathop{\rm tanx}\nolimits} = tan\dfrac{{3\pi }}{{11}} \Leftrightarrow x = \dfrac{{3\pi }}{{11}} + k\pi \Rightarrow \dfrac{{3\pi }}{{11}} + k\pi \in \left( {\dfrac{\pi }{4};2\pi } \right) \Rightarrow k = 0,k = 1\)
Chọn B

Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(tan^2x-4tanx+3=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(tanx-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}tanx=1\\cotx=\frac{1}{3}\end{matrix}\right.\)

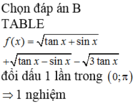
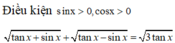
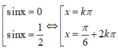
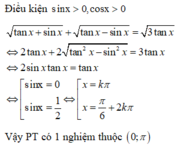
\(tanx=tan\left(\dfrac{3\pi}{11}\right)\Leftrightarrow x=\dfrac{3\pi}{11}+k\pi\)
\(\dfrac{\pi}{4}< x< 2\pi\Rightarrow\dfrac{\pi}{4}< \dfrac{3\pi}{11}+k\pi< 2\pi\)
\(\Rightarrow-\dfrac{1}{44}< k< \dfrac{19}{11}\Rightarrow k=\left\{0;1\right\}\)
\(\Rightarrow\) Phương trình có 2 nghiệm trên khoảng đã cho (ứng với 2 giá trị của k)
em cảm ơn cô ạ