Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Sau khi bớt ở phân số thứ nhất 1/3sau khi bớt ở phân số thứ nhất đi 1/3 và phân số thứ hai đi 3/8 thì tổng hai phân số là 7/9 tính tổng hai phân số ban đầu là 1/3 + 3/8 - 7/8 = ?
Sau khi bớt ở phân số thứ nhất đi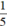 
thì tổng 2 phân số ban đầu cũng giảm đi 
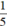và bằng 
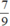. Vậy tổng 2 phân số ban đầu là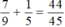 
Sau khi bớt ở phân số thứ nhất đi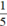 
thì tổng 2 phân số ban đầu cũng giảm đi 
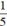và bằng 
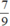. Vậy tổng 2 phân số ban đầu là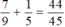 
Tổng mới hai phân số đó là :
\(\frac{5}{19}+\frac{1}{19}+\frac{2}{19}=\frac{8}{19}\)
ĐS : . . .
tổng mới là:
5/19 + 1/19 + 2/19 = 8/19
đáp số: 8/19
k nha
Tổng của ba phân số đó là : \(\left(\frac{31}{24}+\frac{7}{8}+\frac{11}{12}\right)\div2=\frac{37}{24}\)
Phân số thứ nhất là : \(\frac{37}{24}-\frac{7}{8}=\frac{2}{3}\)
Phân số thứ hai là : \(\frac{37}{24}-\frac{11}{12}=\frac{5}{8}\)
Phân số thứ ba là : \(\frac{37}{24}-\frac{31}{24}=\frac{1}{4}\)
#Death.Hunter
tổng:4/5 + 2/5 =38/35
hiệu:4/5 - 2/7 = 18/35
tích: 4/5 x 2/7 + 8/35
thương:4/5 : 2/7 = 14/5
Mình sẽ giải từng câu
Bài 1 :
Ta có :
\(\frac{45-m}{67+m}=\frac{5}{9}\)
\(\Leftrightarrow\)\(9\left(45-m\right)=5\left(67+m\right)\)
\(\Leftrightarrow\)\(405-9m=335+5m\)
\(\Leftrightarrow\)\(5m+9m=405-335\)
\(\Leftrightarrow\)\(14m=70\)
\(\Leftrightarrow\)\(m=\frac{70}{14}\)
\(\Leftrightarrow\)\(m=5\)
Vậy số tự nhiên m cần tìm là \(m=5\)
Chúc bạn học tốt ~
Một người bán trứng đi chợ bán . Lần thứ nhất bán được 1/3 số trứng , lần thứ hai bán tiếp được2/3 số trứng còn lại thì còn 12 quả . Hỏi lúc đầu người đó mang đi chợ ... Phân số chỉ số phần số trứng còn lại sau khi bán lần thứ nhất là : 1 - 1/3 = 2/3 ( số trứng ). Phân số chỉ số phần số trứng bán lần hai là : 2/3 x 2/3 = 4/9 ( số ...
Tổng 2 phân số ban đầu là : 7/9 + 1/5 = 44/45
Đáp số : 44/45
Nhớ tk cho mình !
Sau khi bớt ở phân số thứ nhất đi \(\frac{1}{5}\)thì tổng của 2 phân số ban đầu cũng giảm đi \(\frac{1}{5}\)và bằng \(\frac{7}{9}\). Vậy tổng hai phân số ban đầu là
\(\frac{7}{9}\)+\(\frac{1}{5}\)=\(\frac{44}{45}\)
Đáp số \(\frac{44}{45}\)