Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\dfrac{-5}{6}=\dfrac{-20}{24};\dfrac{7}{8}=\dfrac{21}{24};\dfrac{7}{24}=\dfrac{7}{24};\dfrac{-3}{4}=-\dfrac{18}{24};\dfrac{2}{3}=\dfrac{16}{24}\)
Do đó: \(\dfrac{-5}{6}< -\dfrac{3}{4}< \dfrac{7}{24}< \dfrac{2}{3}< \dfrac{7}{8}\)
\(\dfrac{7}{8}=\dfrac{119}{136};\dfrac{16}{17}=\dfrac{128}{136}\)
mà 119<128
nên 7/8<16/17
DO đó: -5/6<-3/4<7/24<2/3<7/8<16/17
b: \(\dfrac{-5}{8}=\dfrac{-95}{8\cdot19};\dfrac{-16}{19}=\dfrac{-128}{19\cdot8}\)
Do đó: -5/8>-16/19
\(\dfrac{7}{10}=0.7;\dfrac{20}{23}\simeq0.87;\dfrac{214}{315}\simeq0.68;\dfrac{205}{107}>1\)
Do đó: \(\dfrac{205}{107}>\dfrac{20}{23}>\dfrac{7}{10}>\dfrac{214}{315}>-\dfrac{5}{8}>-\dfrac{16}{19}\)

A) \(\frac{17}{120}\) ; \(\frac{11}{72}\) ; \(\frac{7}{28}\)
B) \(\frac{-31}{49}\) ; \(\frac{-62}{97}\) ; \(\frac{-63}{97}\) \(\frac{-93}{140}\)


1) \(\dfrac{3}{2}\) : \(\dfrac{9}{4}\) =\(\dfrac{3}{2}\)x\(\dfrac{4}{9}\)=\(\dfrac{12}{18}\)=\(\dfrac{2}{3}\)
2)\(\dfrac{48}{55}\) : \(\dfrac{12}{11}\)= \(\dfrac{48}{55}\) x\(\dfrac{11}{12}\)= \(\)\(\dfrac{528}{660}\)=\(\dfrac{4}{5}\)
3)\(\dfrac{7}{10}\) : \(\dfrac{7}{5}\)=\(\dfrac{7}{10}\) x \(\dfrac{5}{7}\)= \(\dfrac{35}{70}\)=\(\dfrac{1}{2}\)
4)\(\dfrac{6}{7}\) : \(\dfrac{8}{7}\) = \(\dfrac{6}{7}\) x \(\dfrac{7}{8}\) =\(\dfrac{42}{56}\)=\(\dfrac{3}{4}\)
Sắp xếp các thương theo thứ tự tăng dần :\(\dfrac{1}{2}\);\(\dfrac{2}{3}\);\(\dfrac{3}{4}\);\(\dfrac{4}{5}\)
\(\Rightarrow\)\(\dfrac{7}{10}\) : \(\dfrac{7}{5}\) ; \(\dfrac{3}{2}\) :\(\dfrac{9}{4}\) ; \(\dfrac{6}{7}\) : \(\dfrac{8}{7}\) ; \(\dfrac{48}{55}\):\(\dfrac{12}{11}\).

a) Ta có: \(\dfrac{19}{33}=\dfrac{38}{66};\dfrac{6}{12}=\dfrac{1}{2}=\dfrac{33}{66};\dfrac{13}{22}=\dfrac{39}{66}\)
Mà \(\dfrac{33}{66}< \dfrac{38}{66}< \dfrac{39}{66}\Rightarrow\dfrac{6}{12}< \dfrac{19}{33}< \dfrac{13}{22}\)
Vậy các số hữu tỉ được sắp xếp theo thứ tự tăng dần là: \(\dfrac{6}{12};\dfrac{19}{33};\dfrac{13}{22}\)
b) Ta có:
\(\dfrac{-18}{12}=\dfrac{-3}{2}=\dfrac{-105}{70};\dfrac{-10}{7}=\dfrac{-100}{70};\dfrac{-8}{5}=\dfrac{-112}{70}\)
Mà \(\dfrac{-112}{70}< \dfrac{-105}{70}< \dfrac{-100}{70}\Rightarrow\dfrac{-8}{5}< \dfrac{-18}{12}< \dfrac{-10}{7}\)
Vậy các số hữu tỉ được sắp xếp theo thứ tự tăng dần là: \(\dfrac{-8}{5};\dfrac{-18}{12};\dfrac{-10}{7}\)
a. \(\dfrac{19}{33};\dfrac{6}{12};\dfrac{13}{22}\) ( \(MC=132\) )
Quy đồng : \(\dfrac{19}{33}=\dfrac{76}{132}\) ; \(\dfrac{6}{12}=\dfrac{66}{132}\) ; \(\dfrac{13}{22}=\dfrac{78}{132}\)
Vì \(\dfrac{66}{132}< \dfrac{76}{132}< \dfrac{78}{132}\) => \(\dfrac{6}{12}< \dfrac{19}{33}< \dfrac{13}{22}\)
b. \(\dfrac{-18}{12};\dfrac{-10}{7};\dfrac{-8}{5}\) ( \(MC=420\) )
Quy đồng : \(\dfrac{-18}{12}=\dfrac{-630}{420}\) ; \(\dfrac{-10}{7}=\dfrac{-600}{420}\) ; \(\dfrac{-8}{5}=\dfrac{-672}{420}\)
Vì : \(\dfrac{-672}{420}< \dfrac{-630}{420}< \dfrac{-600}{420}\) => \(\dfrac{-8}{5}< \dfrac{-18}{12}< \dfrac{-10}{7}\)

\(a,\dfrac{-5}{8};\dfrac{7}{10};\dfrac{16}{19};\dfrac{20}{23}\)
\(\Rightarrow\dfrac{20}{23}>\dfrac{16}{19}>\dfrac{7}{10}>\dfrac{-5}{8}\)
Vậy \(\dfrac{20}{23}>\dfrac{16}{19}>\dfrac{7}{10}>\dfrac{-5}{8}\)
\(b,\dfrac{5\times6+6\times7}{5\times5+20}\)và \(\dfrac{8\times9-4\times15}{12\times7-180}\)
Xét : \(\dfrac{5\times6+6\times7}{5\times5+20}\)
\(=\dfrac{\left(5+7\right)\times6}{5\times5+5\times4}\)
\(=\dfrac{12\times6}{\left(5+4\right)\times5}\)
\(=\dfrac{72}{9\times5}\)
\(=\dfrac{72}{45}\)
\(=\dfrac{8}{5}\)
Xét : \(\dfrac{8\times9-4\times15}{12\times7-180}\)
\(=\dfrac{72-60}{84-180}\)
\(=\dfrac{12}{-96}\)
\(=\dfrac{-1}{8}\)
Quy đồng \(\dfrac{8}{5}=\dfrac{8\times8}{5\times8}=\dfrac{64}{40}\\ \dfrac{-1}{8}=\dfrac{\left(-1\right)\times5}{8\times5}=\dfrac{-5}{40}\)
Vì \(\dfrac{64}{40}>\dfrac{-5}{40}\)
\(\Rightarrow\dfrac{8}{5}>\dfrac{-1}{8}\)
\(\Rightarrow\dfrac{5\times6+6\times7}{5\times5+20}>\dfrac{8\times9-4\times15}{12\times7-180}\)
Vậy \(\dfrac{5\times6+6\times7}{5\times5+20}>\dfrac{8\times9-4\times15}{12\times7-180}\)

![]() A = \(\dfrac{17}{15}.\dfrac{-31}{125}.\dfrac{1}{2}.\dfrac{10}{17}.\dfrac{-1}{8}\)
A = \(\dfrac{17}{15}.\dfrac{-31}{125}.\dfrac{1}{2}.\dfrac{10}{17}.\dfrac{-1}{8}\)
= \(\dfrac{17.\left(-31\right).1.10.\left(-1\right)}{15.125.2.17.8}\)
= \(\dfrac{17.\left[\left(-31\right).\left(-1\right)\right].1.2.5}{5.3.125.17.4.2}\)
= \(\dfrac{31.1}{3.125.4}\)
= \(\dfrac{31}{1500}\)
![]() B = \(\left(\dfrac{11}{4}.\dfrac{-5}{9}-\dfrac{4}{9}.\dfrac{11}{4}\right).\dfrac{8}{33}\)
B = \(\left(\dfrac{11}{4}.\dfrac{-5}{9}-\dfrac{4}{9}.\dfrac{11}{4}\right).\dfrac{8}{33}\)
= \(\left[\dfrac{11}{4}.\left(\dfrac{-5}{9}-\dfrac{4}{9}\right)\right].\dfrac{8}{33}\)
= \(\left(\dfrac{11}{4}.\dfrac{-9}{9}\right).\dfrac{8}{33}\)
= \(\left[\dfrac{11}{4}.\left(-1\right)\right].\dfrac{4.2}{\left(-11\right).\left(-3\right)}\)
= \(\dfrac{-11}{4}.\dfrac{4.2}{\left(-11\right).\left(-3\right)}\)
= \(\dfrac{\left(-11\right).4.2}{4.\left(-11\right)\left(-3\right)}\)
= \(\dfrac{2}{-3}\)
Ok nhá!

A=\(\dfrac{2}{7}+\dfrac{-3}{8}+\dfrac{11}{7}+\dfrac{1}{3}+\dfrac{1}{7}+\dfrac{5}{-3}\)
A=\(\left(\dfrac{2}{7}+\dfrac{11}{7}+\dfrac{1}{7}\right)+\left(\dfrac{1}{3}+\dfrac{5}{-3}\right)+\dfrac{-3}{8}\)
A=\(2+\dfrac{-4}{3}+\dfrac{-3}{8}\)
A=\(\dfrac{7}{24}\)
B=\(\left(\dfrac{3}{17}+\dfrac{14}{17}\right)+\left(\dfrac{-18}{35}+\dfrac{17}{-35}\right)+\left(\dfrac{-5}{13}+\dfrac{-8}{13}\right)\)
B=\(\dfrac{17}{17}+\dfrac{-35}{35}+\dfrac{-13}{13}\)
B=\(1+\left(-1\right)+\left(-1\right)=-1\)
C=\(\dfrac{-3}{17}+\left(\dfrac{2}{3}+\dfrac{3}{17}\right)\)
C=\(\dfrac{-3}{17}+\dfrac{2}{3}+\dfrac{3}{17}=\left(\dfrac{-3}{17}+\dfrac{3}{17}\right)+\dfrac{2}{3}\)
C=0+\(\dfrac{2}{3}=\dfrac{2}{3}\)
D=\(\left(\dfrac{-1}{6}+\dfrac{5}{-12}\right)+\dfrac{7}{12}\)
D=\(\dfrac{-1}{6}+\dfrac{5}{-12}+\dfrac{7}{12}\)
D=\(\dfrac{-2}{12}+\dfrac{-5}{12}+\dfrac{7}{12}=\left(\dfrac{-2}{12}+\dfrac{-5}{12}\right)+\dfrac{7}{12}\)
D=\(\dfrac{-7}{12}+\dfrac{7}{12}=0\)
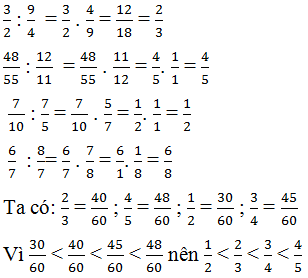
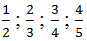
Giải:
a)
\(\dfrac{7}{48}=\dfrac{105}{720};\)
\(\dfrac{11}{72}=\dfrac{110}{720};\)
\(\dfrac{17}{120}=\dfrac{102}{720}\)
Vì \(102< 105< 110\)
\(\Leftrightarrow\dfrac{102}{720}< \dfrac{105}{720}< \dfrac{110}{720}\)
\(\Leftrightarrow\dfrac{17}{120}< \dfrac{7}{48}< \dfrac{11}{72}\)
Vậy ...
b) \(\dfrac{31}{49}=\dfrac{60140}{95060};\)
\(\dfrac{62}{97}=\dfrac{60760}{95060};\)
\(\dfrac{93}{140}=\dfrac{63147}{95060}\)
Vì \(60140< 60760< 63147\)
\(\Leftrightarrow\dfrac{60140}{95060}< \dfrac{60760}{95060}< \dfrac{63147}{95060}\)
\(\Leftrightarrow\dfrac{31}{49}< \dfrac{62}{97}< \dfrac{93}{140}\)
Vậy ...
a ) \(\dfrac{7}{48}\) = \(\dfrac{105}{720}\)
\(\dfrac{11}{72}\) = \(\dfrac{110}{720}\)
\(\dfrac{17}{120}\) = \(\dfrac{102}{720}\)
Vì 102 < 105 < 110
\(\Leftrightarrow\) \(\dfrac{102}{720}\) < \(\dfrac{105}{720}\) < \(\dfrac{110}{720}\)
\(\Leftrightarrow\) \(\dfrac{17}{120}\) < \(\dfrac{7}{48}\) < \(\dfrac{11}{72}\)
Vậy .....................
( k cho tớ nha . Tớ chỉ bt lm phần a )