Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(\frac{2x^2+1}{x^2-1}-\frac{1}{x-1}\right):\left(1-\frac{x^2+4}{x^2+x+1}\right)\)
\(=\left[\frac{2x^2+1}{\left(x-1\right)\left(x+1\right)}-\frac{x+1}{\left(x-1\right)\left(x+1\right)}\right]:\frac{x^2+x+1-x^2-4}{x^2+x+1}\)
\(=\frac{2x^2+1-x-1}{\left(x-1\right)\left(x+1\right)}:\frac{x-3}{x^2+x+1}\)
\(=\frac{2x^2-x}{\left(x-1\right)\left(x+1\right)}.\frac{x^2+x+1}{x-3}\)
bài này đến đây cậu làm tiếp chư tôi ko tách ra đc nữa

a: \(P=\dfrac{4x-6-x+1}{2x-3}:\left(\dfrac{6x+1}{2x^2-3x+2x-3}+\dfrac{x}{x+1}\right)\)
\(=\dfrac{3x-5}{2x-3}:\left(\dfrac{6x+1}{\left(x+1\right)\left(2x-3\right)}+\dfrac{x}{x+1}\right)\)
\(=\dfrac{3x-5}{2x-3}:\dfrac{6x+1+2x^2-3x}{\left(x+1\right)\left(2x-3\right)}\)
\(=\dfrac{3x-5}{\left(2x-3\right)}\cdot\dfrac{\left(2x-3\right)\left(x+1\right)}{2x^2+3x+1}\)
\(=\dfrac{3x-5}{2x+1}\)
b: \(P-\dfrac{3}{2}=\dfrac{3x-5}{2x+1}-\dfrac{3}{2}=\dfrac{6x-10-6x-3}{2\left(2x+1\right)}=\dfrac{-7}{2\left(2x+1\right)}\)

a)\(P=\left[\frac{2}{\left(x+1\right)^3}.\left(\frac{1}{x}+1\right)+\frac{1}{x^2+2x+1}.\left(\frac{1}{x^2}+1\right)\right]:\frac{x-1}{x^3}\left(ĐKXĐ:x\ne0;-1\right)\)
\(P=\left[\frac{2}{\left(x+1\right)^3}.\left(\frac{x+1}{x}\right)+\frac{1}{\left(x+1\right)^2}.\left(\frac{x^2+1}{x^2}\right)\right]:\frac{x-1}{x^3}\)
\(P=\left[\frac{2}{\left(x+1\right)^2x}+\frac{x^2+1}{\left[x\left(x+1\right)\right]^2}\right]:\frac{x-1}{x^3}\)
\(P=\left[\frac{x^2+2x+1}{\left[x\left(x+1\right)\right]^2}\right]:\frac{x-1}{3}\)
\(P=\frac{\left(x+1\right)^2}{x^2\left(x+1\right)^2}:\frac{x-1}{3}\)
\(P=\frac{3}{x^2\left(x-1\right)}\)
b)Bài này liên quan đến dấu lớn nên mk ko làm đc

\(\left(\frac{1}{x+1}-\frac{3}{x^3+1}+\frac{3}{x^2-x+1}\right):\frac{3x^2-3x+3}{\left(x+1\right)\left(x+2\right)}-\frac{2x-2}{x^2+2x}\left(x\ne-1;x\ne0;x\ne-2\right)\)
\(=\left(\frac{1}{x+1}-\frac{3}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{3}{x^2-x+1}\right):\frac{3x^3-3x+3}{\left(x+1\right)\left(x+2\right)}-\frac{2\left(x-1\right)}{x\left(x+2\right)}\)
\(=\left(\frac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}-\frac{3}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{3x+3}{\left(x+1\right)\left(x^2-x+1\right)}\right)\)\(:\frac{3x^2-3x+3}{\left(x+1\right)\left(x+2\right)}-\frac{2\left(x-1\right)}{x\left(x+2\right)}\)
\(=\frac{x^2-x+1-3+3x+3}{\left(x+1\right)\left(x^2-x+1\right)}:\frac{3x^2-3x+3}{\left(x+1\right)\left(x+2\right)}-\frac{2\left(x-1\right)}{x\left(x+2\right)}\)
\(=\frac{x^2+2x+1}{\left(x+1\right)\left(x^2-x+1\right)}:\frac{3\left(x^2-x+1\right)}{\left(x+1\right)\left(x+1\right)}-\frac{2\left(x-1\right)}{x\left(x+2\right)}\)
\(=\frac{\left(x+1\right)\left(x+2\right)}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\frac{\left(x+1\right)\left(x+2\right)}{3\left(x^2-x+1\right)}-\frac{2\left(x-1\right)}{x\left(x+2\right)}\)
\(=\frac{\left(x+2\right)^2\left(x+1\right)}{3\left(x^2-x+1\right)^2}-\frac{2\left(x-1\right)}{x\left(x+2\right)}\)

\(\left(\frac{1}{x}+1-\frac{3}{x^3+1}-\frac{3}{x^2-x+1}\right)\cdot\frac{3x^2-3x+3}{\left(x+1\right).\left(x+2\right)}-\frac{2x-2}{x^2+2x}\)
\(=\left(\frac{x+1}{x}-\frac{3}{\left(x+1\right).\left(x^2-x+1\right)}+\frac{3.\left(x+1\right)}{\left(x+1\right).\left(x^2-x+1\right)}\right)\cdot\frac{3.\left(x^2-x+1\right)}{\left(x+1\right).\left(x+2\right)}-\frac{2.\left(x-1\right)}{x.\left(x+2\right)}\)
\(=\left[\frac{\left(x+1\right)^2.\left(x^2-x+1\right)-3x+3x^2+3x}{x.\left(x+1\right).\left(x^2-x+1\right)}\right]\cdot\frac{3.\left(x^2-x+1\right)}{\left(x+1\right).\left(x+2\right)}-\frac{2.\left(x-1\right)}{x.\left(x+2\right)}\)
\(=\left[\frac{x^4+x^3+x+1+3x^2}{x.\left(x+1\right).\left(x^2-x+1\right)}\right]\cdot\frac{3.\left(x^2-x+1\right)}{\left(x+1\right).\left(x+2\right)}-\frac{2.\left(x-1\right)}{x.\left(x+2\right)}\)
\(=\frac{3x^4+3x^3+3x+3+9x^2}{x.\left(x+1\right)^2.\left(x+2\right)}-\frac{2.\left(x-1\right)}{x.\left(x+2\right)}=\frac{3x^4+3x^3+3x+3+9x^2}{x.\left(x+1\right)^2.\left(x+2\right)}-\frac{2x^3+2x^2-2x-2}{x.\left(x+1\right)^2.\left(x+2\right)}\)
\(=\frac{3x^4+x^3+7x^2+5x+5}{x.\left(x+1\right)^2.\left(x+2\right)}\)

ĐK: \(\hept{\begin{cases}x\ne1\\x\ne\frac{3}{2}\end{cases}}\)
\(\left(\frac{2x}{2x^2-5x+3}-\frac{5}{2x-3}\right)\div\left(3+\frac{2}{1-x}\right)\)
\(=\frac{2x-5\left(x-1\right)}{\left(2x-3\right)\left(x-1\right)}:\frac{3-3x+2}{1-x}\)
\(=\frac{5-3x}{\left(2x-3\right)\left(x-1\right)}.\frac{1-x}{5-3x}\)
\(=\frac{1}{3-2x}\)
\(\left(\frac{2x}{2x^2-5x+3}-\frac{5}{2x-3}\right):\left(3+\frac{2}{1-x}\right)\)\(ĐKXĐ:x\ne1;x\ne\frac{3}{2}\)
\(=\)\(\left[\frac{2x}{\left(2x-3\right)\left(x-1\right)}-\frac{5\left(x-1\right)}{\left(2x-3\right)\left(x-1\right)}\right]:\left[\frac{3x-3-2}{x-1}\right]\)
\(=\frac{2x-5x+5}{\left(2x-3\right)\left(x-1\right)}:\frac{3x-5}{x-1}\)
\(=\frac{-3x+5}{\left(2x-3\right)\left(x-1\right)}.\frac{x-1}{3x-5}\)
\(=\frac{-\left(3x-5\right)}{2x-3}.\frac{1}{3x-5}\)
\(=\frac{-1}{2x-3}\)
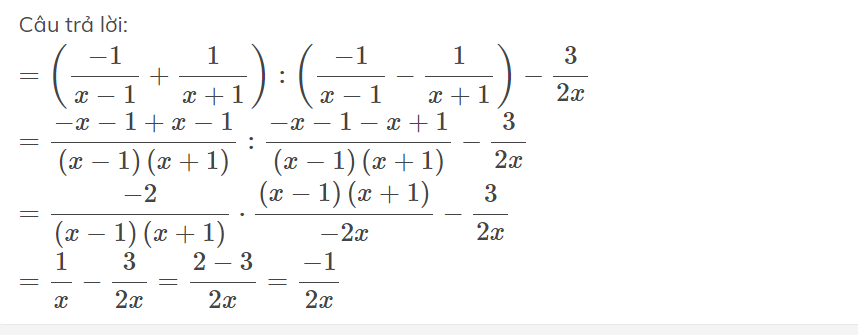
\(=\left(\dfrac{-1}{x-1}+\dfrac{1}{x+1}\right):\left(\dfrac{-1}{x-1}-\dfrac{1}{x+1}\right)-\dfrac{3}{2x}\)
\(=\dfrac{-x-1+x-1}{\left(x-1\right)\left(x+1\right)}:\dfrac{-x-1-x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{3}{2x}\)
\(=\dfrac{-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2x}-\dfrac{3}{2x}\)
\(=\dfrac{1}{x}-\dfrac{3}{2x}=\dfrac{2-3}{2x}=\dfrac{-1}{2x}\)