P
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Q
4 tháng 6 2017
a) \(\sqrt{15+2\sqrt{5}-\sqrt{21-4\sqrt{5}}}\)
\(=\sqrt{15+2\sqrt{5}-\sqrt{\left(1-2\sqrt{5}\right)^2}}\)
\(=\sqrt{15+2\sqrt{5}-\left(2\sqrt{5}-1\right)}\)
\(=\sqrt{15+2\sqrt{5}-\left(2\sqrt{5}-1\right)}\)
\(=\sqrt{15+2\sqrt{5}-2\sqrt{5}+1}\)
\(=\sqrt{16}\)
\(=4\)
b) \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
\(=\sqrt[4]{5-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
\(=\sqrt[4]{5-\sqrt{3-\sqrt{\left(3-2\sqrt{5}\right)^2}}}\)
\(=\sqrt[4]{5-\sqrt{3-\left(2\sqrt{5}-3\right)}}\)
\(=\sqrt[4]{5-\sqrt{3-2\sqrt{5}+3}}\)
\(=\sqrt[4]{5-\sqrt{6-2\sqrt{5}}}\)
\(=\sqrt[4]{5-\sqrt{\left(1-\sqrt{5}\right)^2}}\)
\(=\sqrt[4]{5-\left(\sqrt{5}-1\right)}\)
\(=\sqrt[4]{5-\sqrt{5}+1}\)
\(=\sqrt[4]{6-\sqrt{5}}\)
N
4 tháng 7 2017
* \(\sqrt{2}\)A = \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}+\sqrt{14}=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}+\sqrt{14}=\sqrt{7}-1-\left(\sqrt{7}+1\right)+\sqrt{14}=\sqrt{14}-2\)
=> A = \(\sqrt{7}-\sqrt{2}\)
* B là 6,5 hay 6*5 vậy bạn
nếu 6,5 thì : B cũng nhân \(\sqrt{2}\) biểu thức trở thành
\(\sqrt{2}B=\sqrt{13+2\sqrt{12}}+\sqrt{13-2\sqrt{12}}+4\sqrt{3}=\sqrt{\left(1+\sqrt{12}\right)^2}+\sqrt{\left(\sqrt{12}-1\right)^2}+4\sqrt{3}=1+\sqrt{12}+\sqrt{12}-1+4\sqrt{3}=4\sqrt{3}+4\sqrt{3}=8\sqrt{3}\)
=> B = \(\dfrac{8\sqrt{3}}{\sqrt{2}}=4\sqrt{6}\)
nếu 6*5 thì : bạn tách hai căn đầu thành một biểu thức rồi bình phương lên rồi giải , sau đó trục căn , biểu thức luôn dương nhé , mấy bài này nếu không thể tách thì làm cách này cũng được
* C thì mik chỉ bít pt được nhiu đây thôi , bạn thông cảm nhé\(\sqrt{29-6\sqrt{20}}=\sqrt{\left(\sqrt{20}-3\right)^2}=\sqrt{20}+3=2\sqrt{5}-3\)
* D = \(\sqrt{13-2\cdot2\sqrt{2}\cdot\sqrt{5}}-\sqrt{53+2\cdot2\sqrt{2}\cdot3\sqrt{5}}=\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}-\sqrt{\left(2\sqrt{2}+3\sqrt{5}\right)^2}=2\sqrt{2}-\sqrt{5}-2\sqrt{2}-3\sqrt{5}=-4\sqrt{5}\)
MD
4 tháng 7 2017
Câu C có sai đề ko? Tui sửa đây!
Ta có: \(C=\sqrt{46+6\sqrt{5}}-\sqrt{29-12\sqrt{5}}\)
=> \(C=\sqrt{45+2.3\sqrt{5}+1}-\sqrt{20-2.3.2\sqrt{5}+9}\)
=> \(C=\sqrt{\left(3\sqrt{5}+1\right)^2}-\sqrt{\left(2\sqrt{5}-3\right)^2}\)
=> \(C=\left|3\sqrt{5}+1\right|-\left|2\sqrt{5}-3\right|\)
=> \(C=3\sqrt{5}+1-2\sqrt{5}+3=4+\sqrt{5}\)
19 tháng 1 2019
\(P=\dfrac{\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{2}+\sqrt{3+\sqrt{5}}\right)}+\dfrac{\sqrt{2}\left(3-\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{2}-\sqrt{3-\sqrt{5}}\right)}\)
\(=\dfrac{3\sqrt{2}+\sqrt{10}}{4+\sqrt{6+2\sqrt{5}}}+\dfrac{3\sqrt{2}-\sqrt{10}}{4-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{3\sqrt{2}+\sqrt{10}}{5+\sqrt{5}}+\dfrac{3\sqrt{2}-\sqrt{10}}{5-\sqrt{5}}\)
\(=\dfrac{\left(3\sqrt{2}+\sqrt{10}\right)\left(5-\sqrt{5}\right)+\left(3\sqrt{2}-\sqrt{10}\right)\left(5+\sqrt{5}\right)}{20}\)
\(=\dfrac{15\sqrt{2}-3\sqrt{10}+5\sqrt{10}-5\sqrt{2}+15\sqrt{2}+3\sqrt{10}-5\sqrt{10}-5\sqrt{2}}{20}\)
\(=\dfrac{30\sqrt{2}-10\sqrt{2}}{20}=\dfrac{20\sqrt{2}}{20}=\sqrt{2}\)
\(\)
VT
1
18 tháng 12 2022
a: \(A=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Leftrightarrow A^3=9+4\sqrt{5}+9-4\sqrt{5}+3\cdot A\)
=>A^3-3A-18=0
=>A=3
b: \(B=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}\)
=>\(B^3=5\sqrt{2}+7-5\sqrt{2}+7+3B\)
=>B^3-3B-14=0
=>B=2,82
c: \(C^3=20+14\sqrt{2}-14\sqrt{2}+20-6C\)
=>C^3+6C-40=0
=>C=2,84
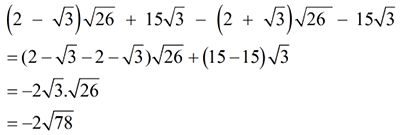
phải đề ghi dầy o nha : \(\sqrt{\sqrt{5-\sqrt{3}}-\sqrt{29-12\sqrt{5}}}\)
sai thôi
Sửa đề: Rút gọn: \(B=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
Giải: Ta có:
\(B=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
\(=\sqrt{\sqrt{5}-\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}}\)
\(=\sqrt{\sqrt{5}-\sqrt{3-2\sqrt{5}+3}}\)
\(=\sqrt{\sqrt{5}-\sqrt{6-2\sqrt{5}}}\)
\(=\sqrt{\sqrt{5}-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\sqrt{\sqrt{5}-\sqrt{5}+1}=\sqrt{1}=1\)
Vậy \(B=1\)