Rút gọn các phân thức sau 2 a 2 - 2 a b a...

Rút gọn các phân thức sau 2 a 2 -...

NN

Nguyễn nhi

23 tháng 12 2023

5.phân thức 4x/3 bằng với phân thức nào sau đây? A. -8x/6 b. 8x/6 c. 7x/6 D. 6/8x 6. Tìm điều kiện xác định của các phân thức sau A) x^2-1/x-2 b) 2x^2+3/x+1 7. Rút gọn các phân thức sau: A) 8x^3yz/24xy^2 b) 12x^4y^2z/x+1 8.thực hiện các phép tính sau: A) x^2+4/3x^2-6x + 5x+2/3x -4x/3x^2-6x

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 12 2023

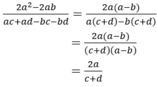
Câu 5: B

Câu 6:

a: ĐKXĐ: \(x-2\ne0\)

=>\(x\ne2\)

b: ĐKXĐ: \(x+1\ne0\)

=>\(x\ne-1\)

8:

\(A=\dfrac{x^2+4}{3x^2-6x}+\dfrac{5x+2}{3x}-\dfrac{4x}{3x^2-6x}\)

\(=\dfrac{x^2+4-4x}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)

\(=\dfrac{\left(x-2\right)^2}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)

\(=\dfrac{x-2+5x+2}{3x}=\dfrac{6x}{3x}=2\)

7:

\(\dfrac{8x^3yz}{24xy^2}\)

\(=\dfrac{8xy\cdot x^2z}{8xy\cdot3y}\)

\(=\dfrac{x^2z}{3y}\)

Đúng(2)

NK

Nguoibian Khongten

2 tháng 10 2015 - olm

Rút gọn biểu thức: A = (a+b+c+d)²+(a+b-c-d)²+(a+c-b-d)²+(a+d-b-c)²

#Toán lớp 8

1

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

2 tháng 10 2015

\(A=\left[\left(a+b\right)+\left(c+d\right)\right]^2+\left[\left(a+b\right)-\left(c+d\right)\right]^2+\left[\left(a-b\right)+\left(c-d\right)\right]^2+\left[\left(a-b\right)-\left(c-d\right)\right]^2\)

Ta có

\(\left[\left(a+b\right)+\left(c+d\right)\right]^2=\left(a+b\right)^2+2\left(a+b\right)\left(c+d\right)+\left(c+d\right)^2\)

\(\left[\left(a+b\right)-\left(c+d\right)\right]^2=\left(a+b\right)^2-2\left(a+b\right)\left(c+d\right)+\left(c+d\right)^2\)

\(\left[\left(a-b\right)+\left(c-d\right)\right]^2=\left(a-b\right)^2+2\left(a-b\right)\left(c-d\right)+\left(c-d\right)^2\)

\(\left[\left(a-b\right)-\left(c-d\right)\right]^2=\left(a-b\right)^2-2\left(a-b\right)\left(c-d\right)+\left(c-d\right)^2\)

\(A=2\left(a+b\right)^2+2\left(a-b\right)^2+2\left(c+d\right)^2+2\left(c-d\right)^2\)

\(A=2\left(a^2+2ab+b^2+a^2-2ab+b^2+c^2+2cd+d^2+c^2-2cd+d^2\right)\)

\(A=4\left(a^2+b^2+c^2+d^2\right)\)

Đúng(1)

L

Linh

2 tháng 12 2018 - olm

Rút gọn các phân thức :

a, \(\frac{\left(a-b\right)\left(c-d\right)}{\left(b^2-a^2\right)\left(d^2-c^2\right)}\)

b, \(\frac{m^4-m}{2m^2+2m+2}\)

#Toán lớp 8

1

PV

Pham Van Hung

2 tháng 12 2018

\(\frac{\left(a-b\right)\left(c-d\right)}{\left(b^2-a^2\right)\left(d^2-c^2\right)}=\frac{\left(b-a\right)\left(d-c\right)}{\left(b-a\right)\left(b+a\right)\left(d-c\right)\left(d+c\right)}=\frac{1}{\left(a+b\right)\left(c+d\right)}\)

\(\frac{m^4-m}{2m^2+2m+2}=\frac{m\left(m^3-1\right)}{2m^2+2m+2}=\frac{m\left(m-1\right)\left(m^2+m+1\right)}{2\left(m^2+m+1\right)}=\frac{m\left(m-1\right)}{2}\)

Đúng(0)

DN

ĐINH NHẬT BẢO NHI

13 tháng 11 2015 - olm

Rút Gọn phân thức sau: {a^3(b^2-c^2)+b^3(c^2-a^2)+c^3(a^2-b^2)}/{a^2(b-c)+b^2(c-a)+c^2(a-b)}

#Toán lớp 8

0

MT

Mai Thành Đạt

25 tháng 11 2016

Rút gọn các phân thức sau :

a ) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}\) b ) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}\)

#Toán lớp 8

2

VD

Võ Đông Anh Tuấn

25 tháng 11 2016

a ) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)

b ) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{a^2+2ab+b^2-c^2}{a^2+2ac+c^2-b^2}\)

\(=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a-b+c}\)

Đúng(0)

HN

Hải Ninh

25 tháng 11 2016

a) \(\frac{\left(a+b\right)^2-c^2}{a+b+c}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{a+b+c}=a+b-c\)

b) \(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ac}=\frac{\left(a^2+2ab+b^2\right)-c^2}{\left(a^2+2ac+c^2\right)-b^2}=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+c+b\right)\left(a+c-b\right)}=\frac{a+b-c}{a+c-b}\)

Đúng(0)

NH

Nguyễn Hoài Phương

21 tháng 1 2017 - olm

rút gọn biêủ thức

(a+b+c+d)²+(a+b-c-d)²+(a+c-b-d)²+(a+d-b-c)²

làm theo các bước nhé đừng có làm tắt

#Toán lớp 8

0

KJ

Kim Jennie

31 tháng 10 2020 - olm

Rút gọn các biểu thức sau

a)(a-b+c+d)(a-b-c-d)

b)(x+2y+3z)(x-2y+3z)

c)(x-1)(x^2-x+1)(x+1)(x^2+x+1)

d)(x^2-2x+1)^3+y^6

#Toán lớp 8

0

PT

phan thị thanh xuân

14 tháng 7 2017 - olm

1) rút gọn các đẳng thức sau

a) (m+n)^2-(m-n)^2+(m+n)(m-n)

b) (a+b)^2-(a-b)^2-2a^3

c) (2x+1)^2+(2x-1)^2+2(4x^2-1)

d) (a+b+c)^2-2(a+b+c)^2(b+c)=(b=+c)^2

#Toán lớp 8

2

LT

lê thị thu huyền

14 tháng 7 2017

a) \(\cdot\left(m+n\right)^2-\left(m-n\right)^2+\left(m+n\right)\left(m-n\right)\)

\(=\left(m+n+m-n\right)\left(m+n-m+n\right)+\left(m+n\right)\left(m-n\right)\)

\(=\left(2m\cdot2n\right)+m^2-n^2\)

\(=4mn+m^2-n^2\)

b) \(\left(a+b\right)^2-\left(a-b\right)^2-2a^3\)

\(=\left(a+b+a-b\right)\left(a+b-a+b\right)-2a^3\)

\(=2ab-2a^3\)

c) \(\left(2x+1\right)^2+\left(2x-1\right)^2+2\left(4x^2-1\right)\)

\(=\left(2x+1\right)^2+2\left(2x+1\right)\left(2x-1\right)+\left(2x-1\right)^2\)

\(=\left(2x+1+2x-1\right)^2\)

\(=\left(4x\right)^2=16x^2\)

d) \(\left(a+b+c\right)^2-2\left(a+b+c\right)\left(b+c\right)+\left(b+c\right)^2\)

\(=\left(a+b+c-b-c\right)^2=a^2\)

Đúng(0)

PT

phan thị thanh xuân

14 tháng 7 2017

xin lỗi mk ghi sai đề ở bài :d) (a+b+c)^2-2(a+b+c)(b+c)+(b+c)^2

Đúng(0)

NP

Nguyễn Phương Linh

11 tháng 7 2015 - olm

Rút gọn biểu thức: D = ( a + b + c + d )²+ ( a + b + c - d )² + (a + b - c - d )² + ( a + d - b - c )²

#Toán lớp 8

1

TN

Trung Nguyen

24 tháng 10 2016

2(a+b)2+2(c+d)2+2(a−b)2+2(d−c)2=2(2a2+2b2+2d2+2c2=4(∑a2)⇔2(a+b)2+2(c+d)2+2(a−b)2+2(d−c)2=2(2a2+2b2+2d2+2c2=4(∑a2)

Đúng(0)

NT

Nguyễn Thảo Nguyên

18 tháng 7 2019 - olm

rút gọn biểu thức:

\(\left(a+b+c+d\right)^2+\left(a+c-c-d\right)^2+\left(a-b+c-d\right)^2+\left(a-b-c+d\right)^2\)

#Toán lớp 8

1

H

headsot96

18 tháng 7 2019

\(\left(a+b+c+d\right)^2+\left(a+b-c-d\right)^2+\left(a-b+c-d\right)^2+\left(a-b-c+d\right)^2\)(Sửa lại nha bn viết sai để)

Đặt x=a+b , y=c+d , z=a-b , t=c-d

Khi đó biểu thức bằng

\(\left(x+y\right)^2+\left(x-y\right)^2+\left(z+t\right)^2+\left(z-t\right)^2\)

\(=x^2+y^2+2xy+x^2+y^2-2xy+z^2+t^2+2zt+z^2+t^2-2zt\)

\(=2\left(x^2+y^2+z^2+t^2\right)=2\left[\left(a+b\right)^2+\left(a-b\right)^2+\left(c+d\right)^2+\left(c-d\right)^2\right]\)

\(=2(a^2+b^2-2ab+a^2+b^2-2ab+c^2+d^2+2cd+c^2+d^2-2cd)\)

\(=2\left(2a^2+2b^2+2c^2+2d^2\right)=4\left(a^2+b^2+c^2+d^2\right)\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP