Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

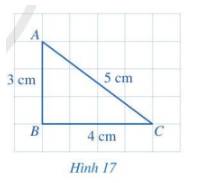
a) Trong tam giác ABC:
\(AB = 3\) cm, \(AC = 5\) cm.
Vậy AB < AC.
b) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).

Em dự đoán cạnh đối diện với góc B lớn hơn cạnh đối diện với góc C.

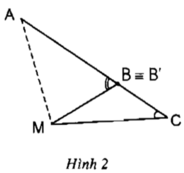
Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C

Do hai tam giác trên có hai cặp góc bằng nhau nên cặp góc còn lại bằng nhau.
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\widehat A = \widehat {A'}\) (gt)
AC = A'C' (gt)
\(\widehat C = \widehat {C'}\) (cmt)
\(\Rightarrow \Delta ABC = \Delta A'B'C'\) (g.c.g)
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.

a) Trong tam giác ABC có \(\widehat B = 90^\circ \)mà tổng ba góc trong một tam giác bằng 180°.
\(\Rightarrow\) Góc C < 90°. Hay \(\widehat B > \widehat C\).
b) Ta có: \(AB = 3\)cm, \(AC = 5\) cm. Vậy AB < AC.