Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

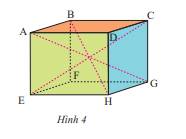
- Các góc ở đỉnh F là: góc BFE, góc BFG, góc EFG
- Các đường chéo được vẽ trong hình là: BH, AG, CE.
- Đường chéo chưa được vẽ là: DF

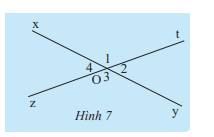
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh

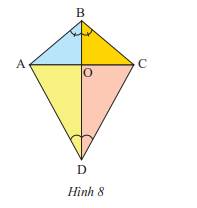
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

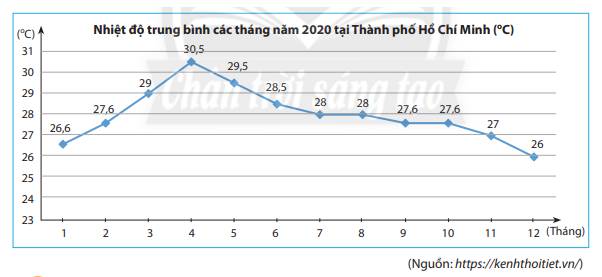
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.

a)
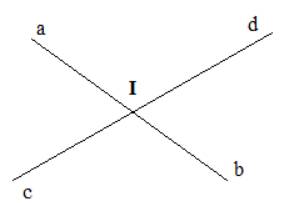
Các cặp góc đối đỉnh trên hình vẽ là: \(\widehat {aId}\) và \(\widehat {bIc}\); \(\widehat {aIc}\) và \(\widehat {bId}\)
b)
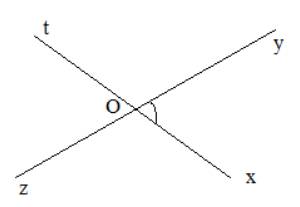
Bước 1: Vẽ góc \(\widehat {xOy}\)
Bước 2: Vẽ tia Ot là tia đối của tia Ox
Bước 3: Vẽ tia Oz là tia đối của tia Oy
Ta được \(\widehat {tOz}\) đối đỉnh với \(\widehat {xOy}\)
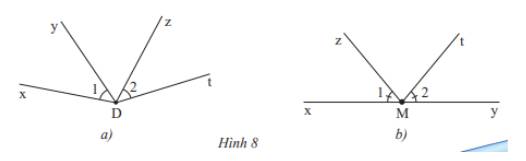
c) Cặp góc \(\widehat {xDy}\) và \(\widehat {zDt}\) trong Hình 8a và cặp góc \(\widehat {xMz}\) và \(\widehat {tMy}\) trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia
Ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy
Ở Hình 8b, My là tia đối của Mx nhưng Mt không là tia đối của Mz
Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
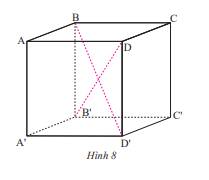




- Vì hình lập phương có tất cả các cạnh bằng nhau, ta có: AB = BC = CD = AD = AA’ = BB’ = CC’ = DD’ = A’B’ = B’C’ = C’D’ = D’A’
Mà AB = 5 cm
Nên BC = CC’ = 5cm
- Các góc ở đỉnh C là: góc BCD, góc BCC’, góc DCC’
- Các đường chéo chưa được vẽ là: AC’ , A’C