Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)
hay \(\widehat {HBA} = \widehat {DCB}\)
Xét \(\Delta ABH\) và \(\Delta DCB\) có:
\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)
\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)
b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).
Xét \(\Delta AEB\) và \(\Delta DCB\) có:
\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)
\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)
Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).

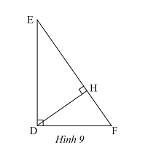
a) Xét \(\Delta DEF\) và \(\Delta HDF\) có:
\(\widehat F\) chung
\(\widehat {EDF} = \widehat {DHF} = 90^\circ \)
Do đó, \(\Delta DEF\backsim\Delta HDF\) (g.g)
b) Vì \(\Delta DEF\backsim\Delta HDF\) nên \(\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
\( \Rightarrow D{F^2} = FH.FE\).
c) Theo câu b ta có:
\(D{F^2} = FH.FE\)
Thay số, \(D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm\)
Vậy \(DF = 9cm\).

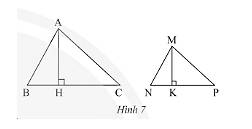
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)

a) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)

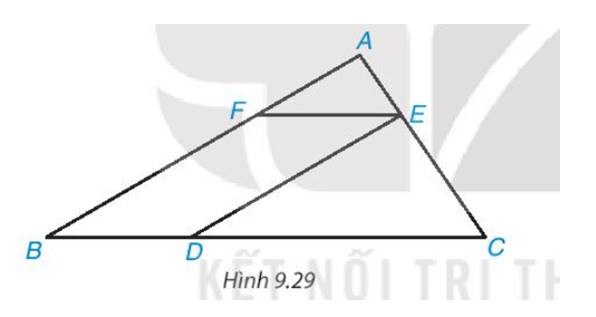
- Có EF // BC => \(\widehat {{\rm{AEF}}} = \widehat {AC{\rm{D}}}\) (2 góc đồng vị) (1)
- Có EF // BD (vì EF // BC)
DE // FB (vì MN // BC)
=> EFBD là hình bình hành
=> \(\widehat {EFB} = \widehat {E{\rm{D}}B}\)
mà \(\widehat {EFB} + \widehat {{\rm{AEF}}} = {180^o}\)
\(\widehat {E{\rm{D}}B} + \widehat {E{\rm{D}}C} = {180^o}\)
=> \(\widehat {AF{\rm{E}}} = \widehat {E{\rm{D}}C}\) (2)
Từ (1) và (2) => ΔAEF ∽ ΔECD (g.g)
Có \(\frac{{AF}}{{E{\rm{D}}}} = \frac{2}{4} = \frac{1}{2}\)
=> Đồng dạng với tỉ số \(\frac{1}{2}\)

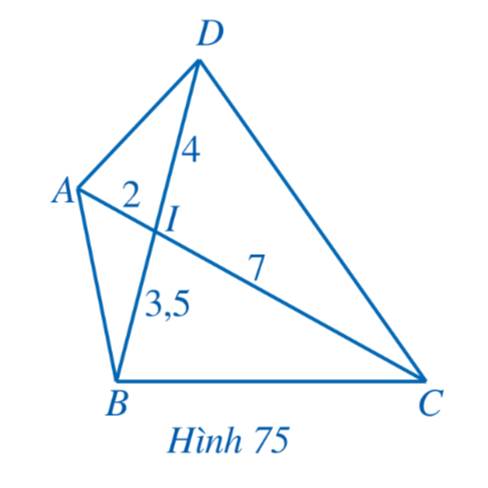
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)

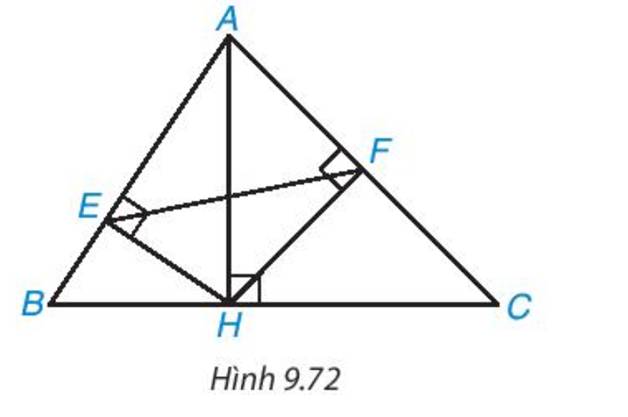
a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có: góc A chung
=> ΔAEH ∽ ΔAHB
b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có: góc A chung
ΔAFH ∽ ΔAHC
c) Vì ΔAEH ∽ ΔAHB nên:
\(\frac{{A{\rm{E}}}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow A{\rm{E}} = \frac{{A{H^2}}}{{AB}}\) (1)
Vì ΔAFH ∽ ΔAHC nên:
\(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF = \frac{{A{H^2}}}{{AC}}\)(2)
Từ (1) và (2) ta có:
\[\frac{{A{\rm{E}}}}{{AF}} = \frac{{AC}}{{AB}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\]
Xét hai tam giác ΔAFE và ΔABC có:
Góc A chung
\[\frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\]
Suy ra ΔAFE ∽ ΔABC (c.g.c)

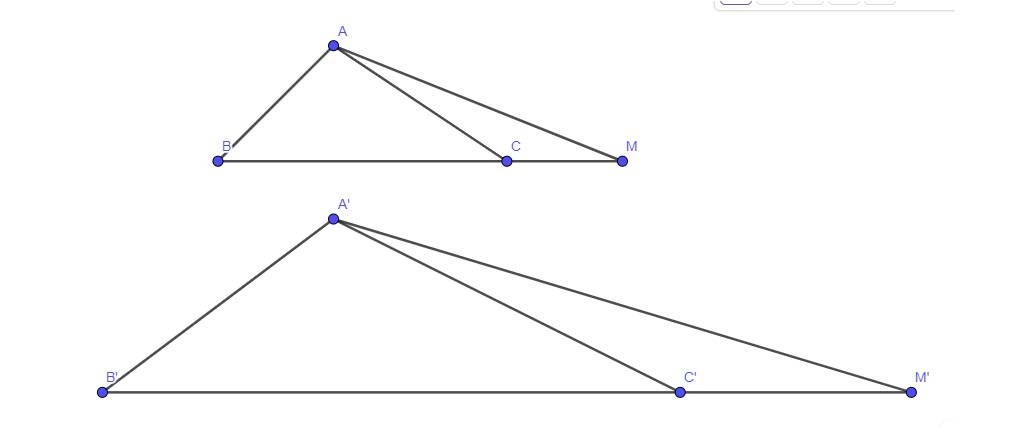
Ta có:
\(\begin{array}{l}\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\\ \Rightarrow \frac{{MB - BC}}{{MB}} = \frac{{M'B' - B'C'}}{{M'B'}}\\ \Rightarrow 1 - \frac{{BC}}{{MB}} = 1 - \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{BC}}{{MB}} = \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{M'B'}}{{MB}} = \frac{{B'C'}}{{BC}}(1)\end{array}\)
Vì ΔA'B'C' ∽ ΔABC suy ra:
\(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}(2)\end{array}\)
Từ (1) và (2) suy ra:
\(\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\)
Xét tam giác ABM và tam giác A”B”M’ có:
\(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\end{array}\)
Suy ra \(\Delta A'B'M' \backsim \Delta ABM\)

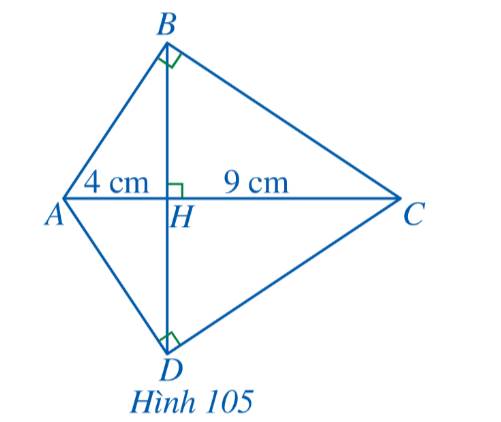
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).
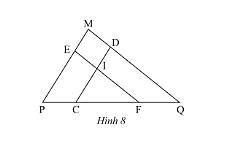


a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).