Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\frac{{AM}}{{MB}} = \frac{1}{2}\)
\(\frac{{AN}}{{AC}} = \frac{{1,5}}{3} = \frac{1}{2}\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.
Xét ∆ABC’ với MN // BC’, ta có:
\( \frac{AM}{MB}=\frac{AN}{NC′}\) (định lí Thalès).
Mà theo câu a, \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) nên ta có \(\frac{{AN}}{{NC}} = \frac{AN}{NC′}\)
Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.
Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.
Vậy đường thẳng d (đi qua M, N) song song với BC.

Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

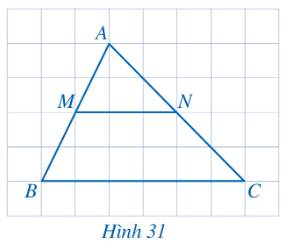
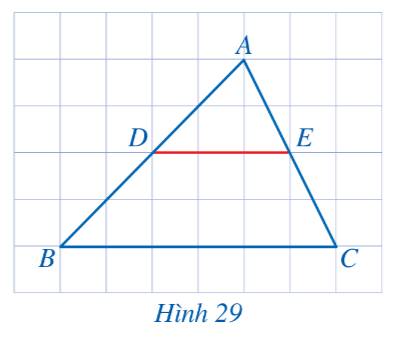
a) Vì MN là đường trung bình của tam giác ABC nên M là trung điểm AB và N là trung điểm AC.
Khi đó \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) suy ra \(MN\parallel BC\) (Định lý Thales đảo trong tam giác ABC).
b) M là trung điểm AB nên \(\frac{{AM}}{{AB}} = \frac{1}{2}\).
Xét tam giác ABC với \(MN\parallel BC\) ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{1}{2}\) (Hệ quả của định lý Thales)

\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)

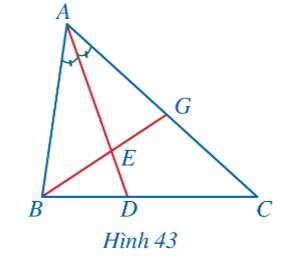
Xét tam giác ABC với đường phân giác AD ta có: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) (Tính chất đường phân giác)
Xét tam giác ABG với đường phân giác AE ta có: \(\frac{{EB}}{{EG}} = \frac{{AB}}{{AG}}\)(Tính chất đường phân giác)
\( \Rightarrow \frac{{DB}}{{DC}}:\frac{{EB}}{{EG}} = \frac{{AB}}{{AC}}:\frac{{AB}}{{AG}} = \frac{{AG}}{{AC}}\) (đpcm)

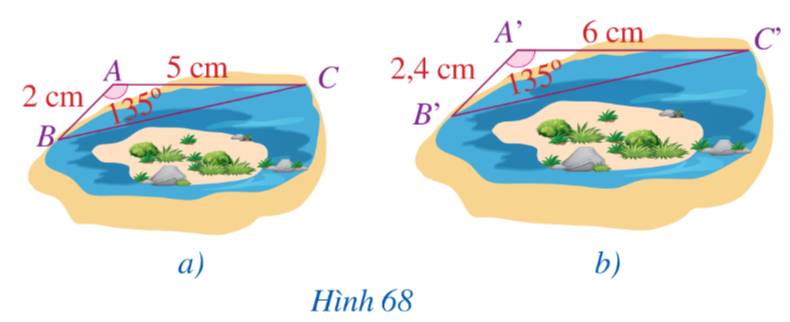
a) Ta có:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{{2,4}} = \frac{5}{6}\\\frac{{A'C'}}{{AC}} = \frac{5}{6}\end{array}\)
Vậy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
b) Ta có: \(\widehat A = \widehat {A'} = 135^\circ \)

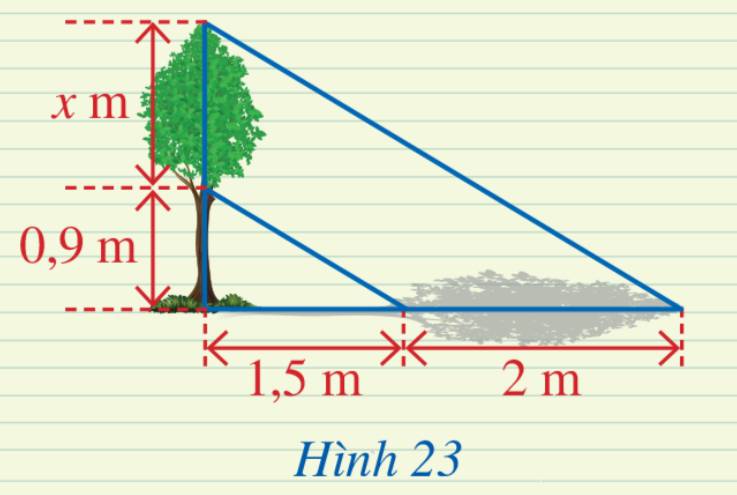
Đoạn thẳng AB biểu thị cho độ cao của cây, đoạn thẳng AD và DB biểu thị độ cao của thân và tán cây, đoạn thẳng AE và EC biểu thị độ dài cái bóng của thân cây và tán cây, đoạn thẳng DE và BC biểu thị cho các tia nắng.
Xét tam giác ABC với \(DE\parallel BC\) ta có:
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) (Định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{0,9}}{x} = \frac{{1,5}}{2}\\ \Rightarrow 0,9.2 = 1,5x\\ \Rightarrow 1,8 = 1,5x\\ \Rightarrow x = 1,2\end{array}\)
Vậy độ cao \(x\) là 1,2 m.

Quan sát hình ta thấy D và trung điểm của đoạn thẳng AB và E là trung điểm của đoạn thẳng AC.

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)
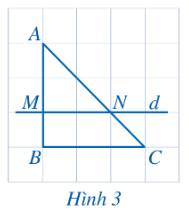


a) Quan sát hình ta thấy \(d\parallel BC\).
b) Ta thấy:
Độ dài AM là 2 lần cạnh của một ô vuông.
Độ dài MB là cạnh của một ô vuông.
\( \Rightarrow \frac{{AM}}{{MB}} = \frac{2}{1} = 2\)
Độ dài AN là 2 lần đường chéo của một ô vuông.
Độ dài NC là độ dài đường chéo của một ô vuông.
\( \Rightarrow \frac{{AN}}{{NC}} = \frac{2}{1} = 2\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).