
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b: Để P nguyên thì \(6\sqrt{x}-4⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}+1\in\left\{1;7\right\}\)
hay \(x\in\left\{0;9\right\}\)

Tổng diện tích của 3 quả bóng l;à:
S1=3*4pi*r^2=12*pi*r^2
Diện tích xung quanh của cái hộp l;à: S2=12*pi*r^2
=>V=S1/S2=1

\(\Leftrightarrow-6\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Vậy \(S=\left\{1;-2\right\}\)
\(\dfrac{x+1}{x}-7=\dfrac{5}{x-2}\)
\(ĐK:x\ne0;2\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x-2\right)-7x\left(x-2\right)}{x\left(x-2\right)}=\dfrac{5x}{x\left(x-2\right)}\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)-7x\left(x-2\right)=5x\)
\(\Leftrightarrow x^2-2x+x-2-7x^2+14-5x=0\)
\(\Leftrightarrow-6x^2-6x+12=0\)
\(\Leftrightarrow-6\left(x^2+x+2\right)=0\)
Ta có: \(x^2+x+2>0;\forall x\)
Vậy pt vô nghiệm

a: Khi m=2 thì (1) sẽ là:
2x+y=2 và 4x+3y=10
=>x=-2 và y=6
b: 2x+y=m và 4x+3y=10
=>4x+2y=2m và 4x+3y=10
=>4x+3y=10 và 4x+2y=2m
=>y=10-2m và 2x=m-10+2m=3m-10
=>y=10-2m và x=3/2m-5
x>0 và y>0
=>10-2m>0 và 3/2m-5>0
=>m>5:3/2=10/3 và m<5
=>10/3<m<5

a,\(\Delta=3^2-4\left(-2\right).6=9+48=57\)
\(x_1=\dfrac{-3+\sqrt{57}}{-4}=\dfrac{3-\sqrt{57}}{4}\)
\(x_2=\dfrac{-3-\sqrt{57}}{-4}=\dfrac{3+\sqrt{57}}{4}\)
b, \(\Delta=6^2-4.3.3=36-36=0\)
\(\Rightarrow x_1=x_2=\dfrac{-6}{2.3}=\dfrac{-6}{6}=-1\)
c, \(\Delta=1^2-4.6.5=1-120=-119< 0\)
Vậy pt vô nghiệm

Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....


a:
ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a< >1\end{matrix}\right.\)
\(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\cdot\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)^2-\left(\sqrt{a}-1\right)^2+4\sqrt{a}\left(a-1\right)}{a-1}\cdot\dfrac{a-1}{\sqrt{a}}\)
\(=\dfrac{a+2\sqrt{a}+1-a+2\sqrt{a}-1+4\sqrt{a}\left(a-1\right)}{\sqrt{a}}\)
\(=\dfrac{4\sqrt{a}+4\sqrt{a}\left(a-1\right)}{\sqrt{a}}\)
=4+4(a-1)
=4a
b: \(a=\left(2+\sqrt{3}\right)\left(\sqrt{3}-1\right)\sqrt{2-\sqrt{3}}\)
\(=\left(2\sqrt{3}-2+3-\sqrt{3}\right)\cdot\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
\(=\left(\sqrt{3}+1\right)\cdot\dfrac{\left(\sqrt{3}-1\right)}{\sqrt{2}}=\dfrac{3-1}{\sqrt{2}}=\sqrt{2}\)
Khi \(a=\sqrt{2}\) thì \(P=4\cdot\sqrt{2}=4\sqrt{2}\)

a: \(A=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+\sqrt{x}+1}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)+1=x-\sqrt{x}+1\)
b:
\(\dfrac{x}{12}=\dfrac{\left(\sqrt{5}+2\right)\sqrt[3]{17\sqrt{5}-38}}{\sqrt{5}+\sqrt{14-6\sqrt{5}}}\)
\(\Leftrightarrow x\cdot\dfrac{1}{12}=\dfrac{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}{\sqrt{5}+3-\sqrt{5}}\)
\(\Leftrightarrow\dfrac{x}{12}=\dfrac{1}{3}\)
=>x=36
Khi x=36 thì \(A=36-6+1=37-6=31\)
c: \(B=\dfrac{2\sqrt{x}}{A}=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
\(B-2=\dfrac{2\sqrt{x}-2x+2\sqrt{x}-2}{x-\sqrt{x}+1}\)
\(=\dfrac{-2x+4\sqrt{x}-2}{x-\sqrt{x}+1}=\dfrac{-2\left(x-2\sqrt{x}+1\right)}{x-\sqrt{x}+1}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}< 0\)
=>B<2
\(2\sqrt{x}>0;x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
=>B>0
=>0<B<2


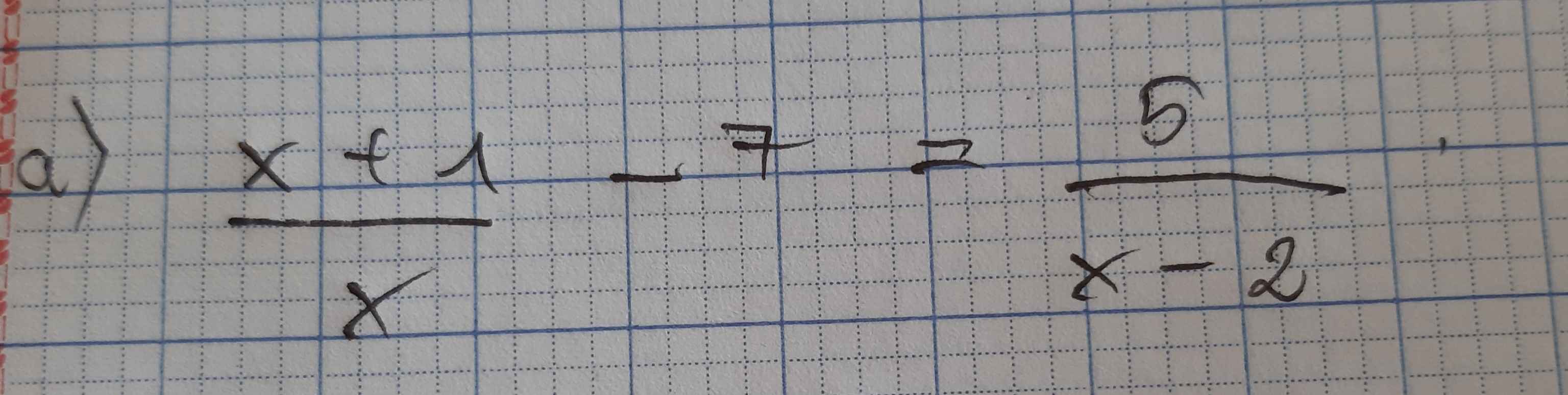

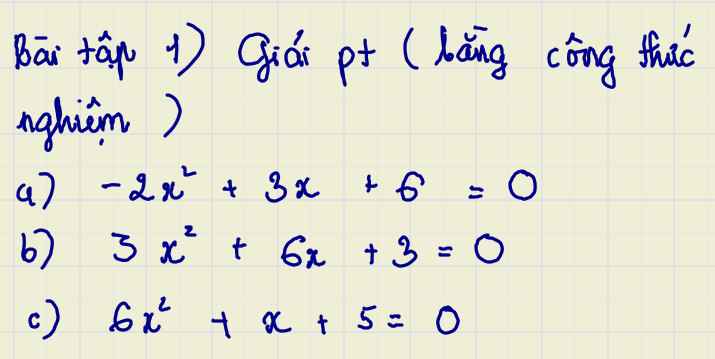

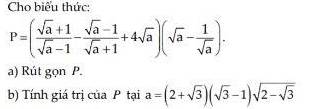

Gọi M( x0 ; y0 ) là điểm cố định mà y luôn đi qua với mọi m
Khi đó : y0 = ( 2m - 3 )x0 + 2m + 1 ∀ m
<=> y0 - 2mx0 + 3x0 - 2m - 1 = 0 ∀ m
<=> -2m( x0 + 1 ) + ( y0 - 1 ) = 0 ∀ m
<=> x0 + 1 = 0 và y0 - 1 = 0 <=> x0 = -1 ; y0 = 1
Vậy y luôn đi qua điểm cố định M( -1 ; 1 )