K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B1
30 tháng 7 2017
1) Ta có BC = BD + DC = 15 + 20 = 35cm
AB / AC = BD / DC = 15 / 20 = 3/4
<=> AB = 3/4.AC
Áp dụng Pytago :
AB² + AC² = 35²
<=> (3/4AC)² + AC² = 35²
<=> 0,5625AC² + AC² = 35²
<=> 1,5625AC² = 35²
<=> AC² = 35² / 1,5625 = 784
<=> AC = 28 cm
=> AB = 3/4 . 28 =21 cm
Cos C = 21 / 35 = 3/5
AD² = AC² + DC² - 2.AC.DC.cosC
<=> AD² = 28² + 20² - 2.28.20.3/5
<=> AD = 16√2 cm = 22,63 cm
quá dễ dàng
động não đi
O
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
2
26 tháng 9 2021
a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)
TH
1
16 tháng 6 2023
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
TN
1
HN
3
12 tháng 9 2021
đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)
MH
9 tháng 4 2022
Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2022
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)
VT
1
13 tháng 11 2021
2: Thay x=1 và y=-4 vào (d), ta được:
2m+2=-4
hay m=-3
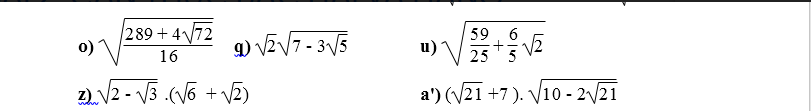
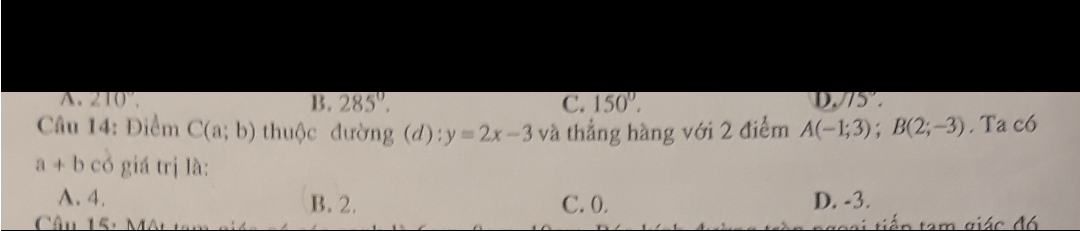
\(1-\sin^2\alpha=\sin^2\alpha+\cos^2\alpha-\sin^2\alpha=\cos^2\alpha\)
\(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)=1-\cos^2\alpha=\sin^2\alpha+\cos^2\alpha-\cos^2a=\sin^2a\)
\(1+\sin^2a+\cos^2\alpha=1+1=2\)
\(\sin\alpha-\sin\alpha\cdot\cos^2\alpha=\sin\alpha\left(1-\cos^2a\right)=\sin\alpha\left(\sin^2\alpha+\cos^2a-\cos^2a\right)=\sin^3\alpha\)
\(\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha\cdot\cos^2\alpha=\left(\sin^2\alpha+\cos^2\alpha\right)^2=1^2=1\)
1/ \(1-\sin^2\alpha=\cos^2\alpha\)
2/ \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)=1-\cos^2\alpha=\sin^2\alpha\)
3/ \(1+\sin^2\alpha+\cos^2\alpha=1+1=2\)
4/ \(\sin\alpha\left(1-\cos^2\alpha\right)=\sin\alpha.\sin^2\alpha=\sin^3\alpha\)
5/ \(=\left(\sin^2\alpha+\cos^2\alpha\right)^2=1\)