Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có BM/BC=BD/BA
nên MD//AC
=>MM' vuông góc AB
=>M đối xứngM' qua AB
b: Xét tứ giác AMBM' có
D là trung điểm chung của AB và MM'
MA=MB
Do đó: AMBM' là hình thoi

a: ĐKXĐ: x<>2; x<>-3
b: \(P+\dfrac{x^2-4-5-x-3}{\left(x-2\right)\left(x+3\right)}=\dfrac{\left(x-4\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}=\dfrac{x-4}{x-2}\)
c: Để P=-3/4 thì x-4/x-2=-3/4
=>4x-8=-3x+6
=>7x=14
=>x=2(loại)
e: x^2-9=0
=>x=3 (nhận) hoặc x=-3(loại)
Khi x=3 thì \(P=\dfrac{3-4}{3-2}=-1\)

1) \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)
2) \(\left(2x-3\right)^2=4x^2-12x+9\)
\(\left(3x-2\right)^2=9x^2-12x+4\)
\(\left(2x-5\right)^2=4x^2-20x+25\)
\(\left(2x-\dfrac{1}{3}\right)^2=4x^2-\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x-\dfrac{1}{3}\right)^2=9x^2-2x+\dfrac{1}{9}\)
3) \(\left(2x-3\right)\left(2x+3\right)=4x^2-9\)
\(\left(3x-4\right)\left(3x+4\right)=9x^2-16\)
\(\left(2x-5\right)\left(2x+5\right)=4x^2-25\)
\(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)=x^2-\dfrac{1}{4}\)
\(\left(2x-\dfrac{1}{3}\right)\left(2x+\dfrac{1}{3}\right)=4x^2-\dfrac{1}{9}\)
1: \(\left(2x+3\right)^2=4x^2+12x+9\)
\(\left(3x+2\right)^2=9x^2+12x+4\)
\(\left(2x+5\right)^2=4x^2+20x+25\)
\(\left(2x+\dfrac{1}{3}\right)^2=4x^2+\dfrac{4}{3}x+\dfrac{1}{9}\)
\(\left(3x+\dfrac{1}{3}\right)^2=9x^2+2x+\dfrac{1}{9}\)

vì đây là câu hỏi hok hành nên là các bạn ghi nội quy là các bạn sai nhé

\(\dfrac{x+9}{x^2-9}-\dfrac{3}{x^2+3x}\)
\(=\dfrac{x+9}{\left(x-3\right)\left(x+3\right)}-\dfrac{3}{x\left(x+3\right)}\)
\(=\dfrac{x\left(x+9\right)}{x\left(x-3\right)\left(x+3\right)}-\dfrac{3\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+6x+9}{x\left(x-3\right)\left(x+3\right)}=\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}=\dfrac{x+3}{x\left(x-3\right)}\)
______________________________________________________
\(\dfrac{x+1}{2x+6}-\dfrac{x-6}{2x^2+6x}\)
\(=\dfrac{x+1}{2\left(x+3\right)}-\dfrac{x-6}{2x\left(x+3\right)}\)
\(=\dfrac{x\left(x+1\right)}{2x\left(x+3\right)}-\dfrac{x-6}{2x\left(x+3\right)}\)
\(=\dfrac{x^2+x-x+6}{2x\left(x+3\right)}=\dfrac{x^2+6}{2x\left(x+3\right)}\)

11)
\(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^{2^{ }}-4}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^2-2^2}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{\left(x-2\right)\left(x+2\right)}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{x\left(x-3\right)}{2}\)

a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)




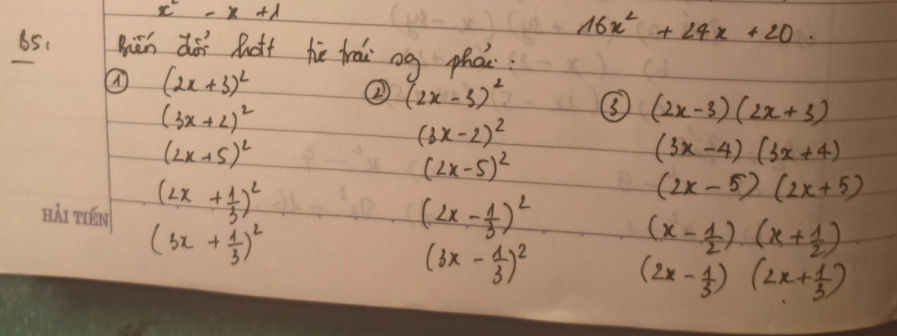

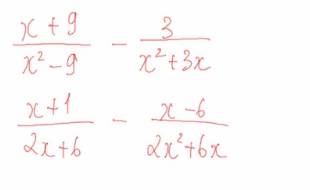
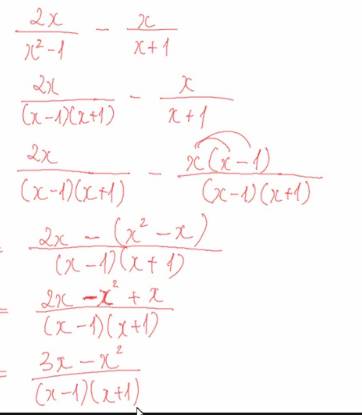



hai bài câu a mik lm đc r nhe mn lm giúp mik câu b thôi ạ mik ko bt lm;-;
Bài 3:
\(a,=-\left(x^2-2x+1\right)-2=-\left(x-1\right)^2-2\le-2\)
Dấu \("="\Leftrightarrow x=1\)
\(b,=-2\left(x^2+2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)+\dfrac{9}{8}=-2\left(x+\dfrac{1}{4}\right)^2+\dfrac{9}{8}\le\dfrac{9}{8}\)
Dấu \("="\Leftrightarrow x=-\dfrac{1}{4}\)
Bài 4:
\(a,=\left(x^2+2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{21}{4}=\left(x+\dfrac{5}{2}\right)^2-\dfrac{21}{4}\ge-\dfrac{21}{4}\)
Dấu \("="\Leftrightarrow x=-\dfrac{5}{2}\)
\(b,=\left(x^2-8x+16\right)+1=\left(x-4\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow x=4\)