Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ĐK: \(\cos x\ne0\)( vì tan x = sinx/cosx nên cos x khác 0)
<=> \(x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
b) ĐK: \(1+\cos2x\ne0\Leftrightarrow\cos2x\ne-1\Leftrightarrow2x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
=> TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
c) ĐK: \(\hept{\begin{cases}\cot x-\sqrt{3}\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\frac{\pi}{6}+k\pi\text{}\text{}\\x\ne l\pi\end{cases}}\); k,l thuộc Z
=>TXĐ: ....
d) ĐK: \(1-2\sin^2x\ne0\Leftrightarrow\cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
=> TXĐ:...


1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)

41.
Số hạng tổng quát của khai triển \(\left(x^2+x\right)^{10}\):
\(T_{k+1}=C^k_{10}.\left(x^2\right)^{10-k}.x^k=C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}\)

Ta có: sinx/2-cosx/2=1/2
<=> (sinx/2-cosx/2)2=1/4
<=> 1- sinx= 1/4
<=> sinx = 3/4
=> cosx = căn7/4 hoặc cosx= -căn7/4
=> sin2x = 2sinx.cosx
=> sin2x = 3. căn7/8 hoặc sin2x=-3.căn7/8

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.




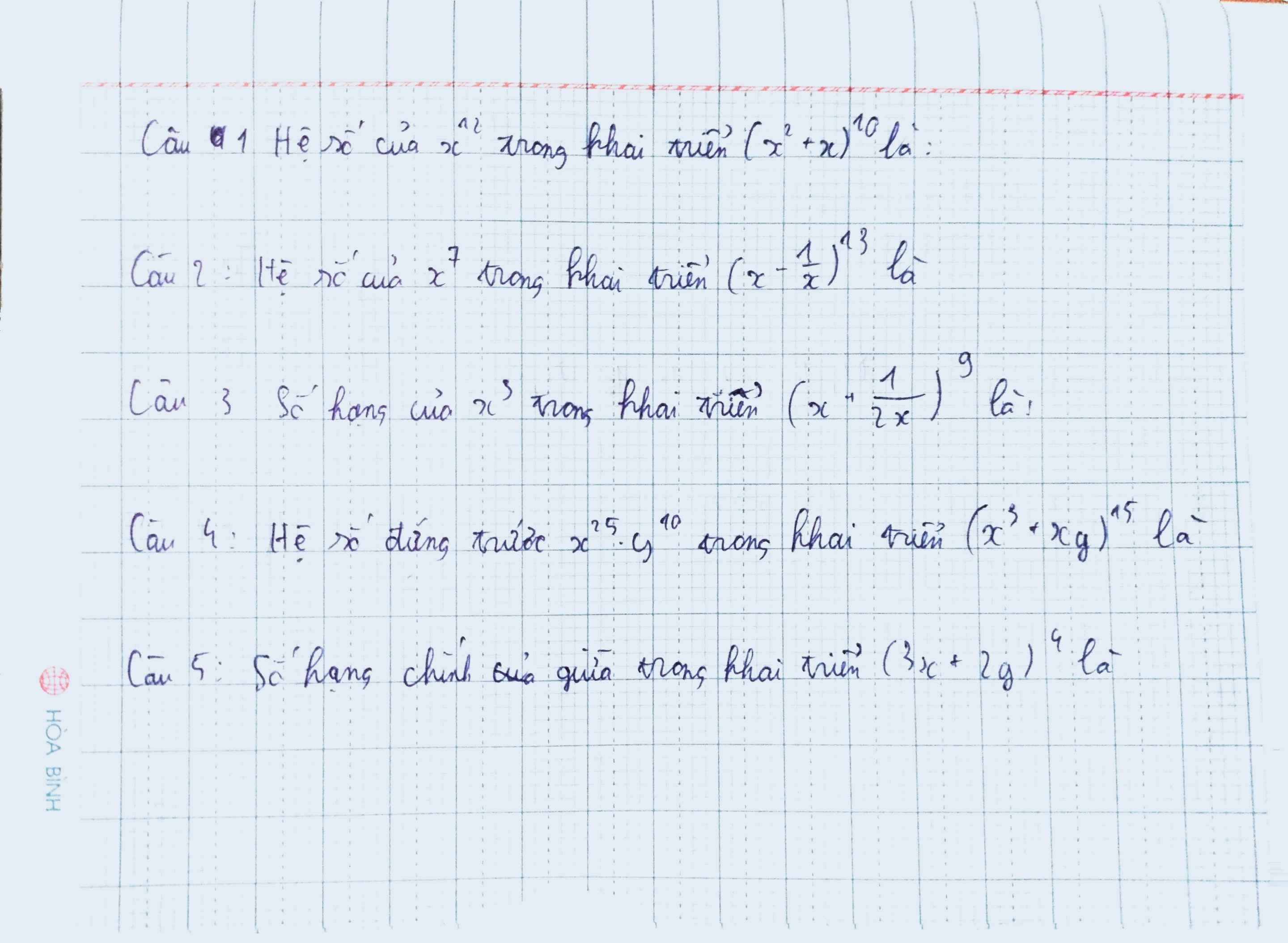

4.
\(u_{n+1}=\dfrac{u_n}{3u_n+1}\Rightarrow\dfrac{1}{u_{n+1}}=\dfrac{3u_n+1}{u_n}=\dfrac{1}{u_n}+3\)
Đặt \(\dfrac{1}{u_n}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{u_1}=2\\v_{n+1}=v_n+3\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số cộng với công bội \(d=3\)
\(\Rightarrow v_n=v_1+\left(n-1\right)d=2+3\left(n-1\right)=3n-1\)
\(\Rightarrow u_n=\dfrac{1}{v_n}=\dfrac{1}{3n-1}\)
6.
\(u_{n+1}=4u_n-3u_{n-1}\Leftrightarrow u_{n+1}-u_n=3\left(u_n-u_{n-1}\right)\)
Đặt \(u_{n+1}-u_n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_2-u_1=3\\v_n=3v_{n-1}\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số nhân với công bội \(q=3\)
\(\Rightarrow v_n=3.3^{n-1}=3^n\)
\(\Rightarrow u_{n+1}-u_n=3^n\)
\(\Rightarrow u_{n+1}-\dfrac{1}{2}.3^{n+1}=u_n-\dfrac{1}{2}.3^n\)
Đặt \(u_n-\dfrac{1}{2}.3^n=x_n\Rightarrow\left\{{}\begin{matrix}x_1=u_1-\dfrac{1}{2}.3^1=-\dfrac{1}{2}\\x_{n+1}=x_n\end{matrix}\right.\)
\(\Rightarrow x_{n+1}=x_n=x_{n-1}=...=x_1=-\dfrac{1}{2}\)
\(\Rightarrow u_n-\dfrac{1}{2}.3^n=-\dfrac{1}{2}\Rightarrow u_n=\dfrac{3^n-1}{2}\)