
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
a.
$xy+x\sqrt{y}-\sqrt{y}-1=x\sqrt{y}(\sqrt{y}+1)-(\sqrt{y}+1)=(\sqrt{y}+1)(x\sqrt{y}-1)$
b.
$ab-a\sqrt{b}+b-\sqrt{b}=(ab+b)-(a\sqrt{b}+\sqrt{b})$
$=b(a+1)-\sqrt{b}(a+1)=(a+1)(b-\sqrt{b})=\sqrt{b}(\sqrt{b}-1)(a+1)$

\(B=\dfrac{\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{7}-1-\sqrt{7}-1}{\sqrt{2}}=-\sqrt{2}\)
B=\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)
=>\(B^2=4-\sqrt{7}+4+\sqrt{7}-2\sqrt{\left(4-\sqrt{7}\right)\left(4+\sqrt{7}\right)}=8-2\sqrt{16-7}\)
\(B^2=8-2\sqrt{9}=8-2.3=8-6=2\)
\(\Rightarrow B=\sqrt{2}\) hoặc \(B=-\sqrt{2}\)
Vì \(4-\sqrt{7}< 4+\sqrt{7}\Rightarrow\sqrt{4-\sqrt{7}}< \sqrt{4+\sqrt{7}}\)
\(\Leftrightarrow\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}< 0\)
hay B<0=>B=\(-\sqrt{2}\)

\(x+\sqrt{2-x}\ge2\sqrt{x\sqrt{2-x}}\)
Bìa này không thể dùng cauchy bạn ạ

a,mấy đoạn dấu : dấu+ trong đề hơi khó nhìn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
b, \(P>0=>\dfrac{x-1}{\sqrt{x}}>0=>x-1>0< =>x>1\)(tm)
Vậy \(x>1\) .....
\(\)

Ta có: \(P=1:\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{x-1}\right)\)
\(=1:\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(=1:\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=1:\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)

bạn ơi ! trên này hiếm 2k4 lắm bn ạ ..có , nhìn thấy , cx không giải đc đâu
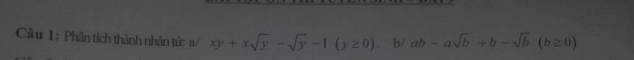 cho mình hỏi bài này
cho mình hỏi bài này

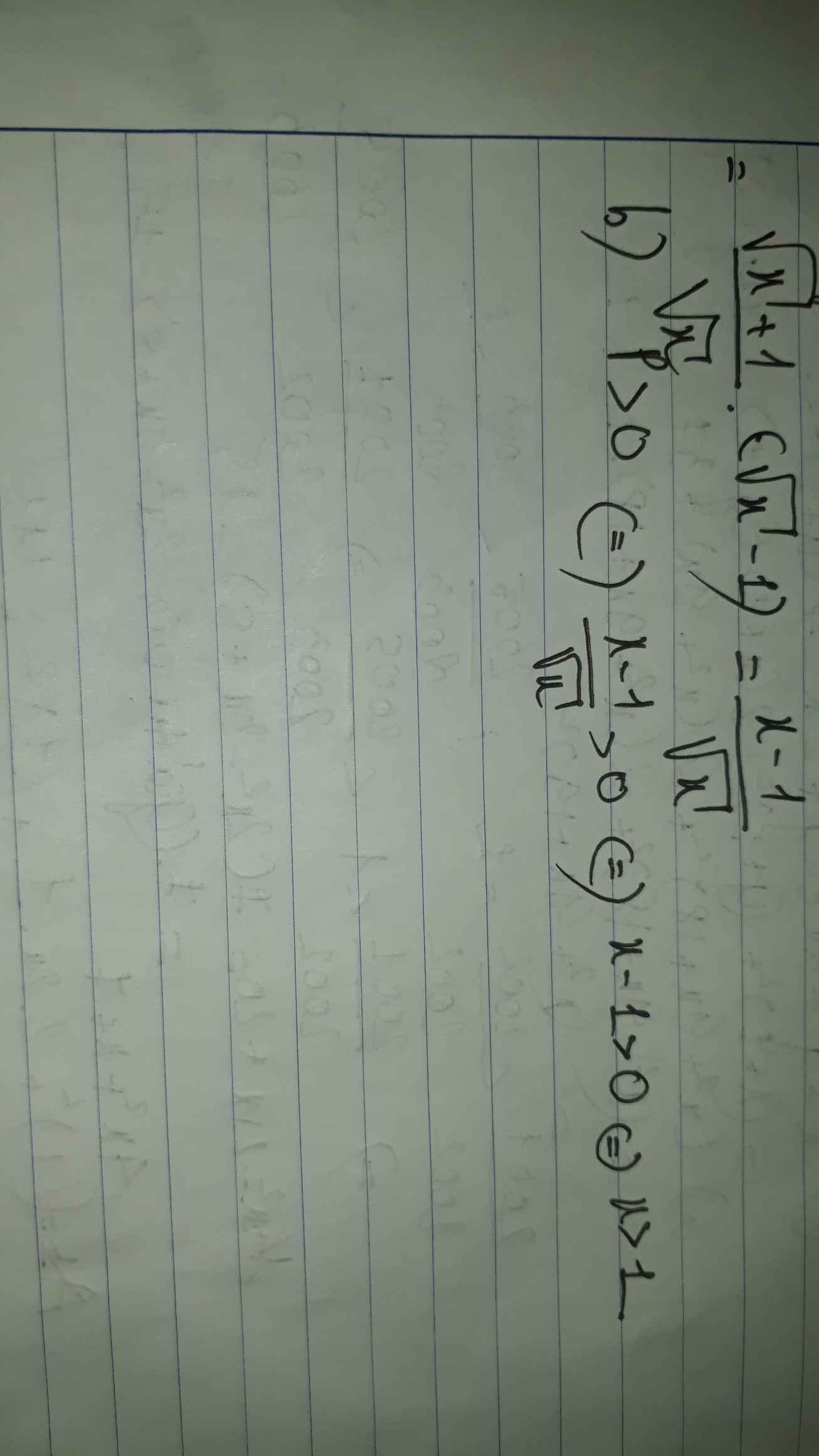
\(A=\sqrt{5}\left(\sqrt{5}-3\right)+\sqrt{45}\)
\(=\sqrt{5}^2-3\sqrt{5}+\sqrt{9.5}\)
\(=\sqrt{5}^2-3\sqrt{5}+3\sqrt{5}\)
\(=\sqrt{5}^2=5\)