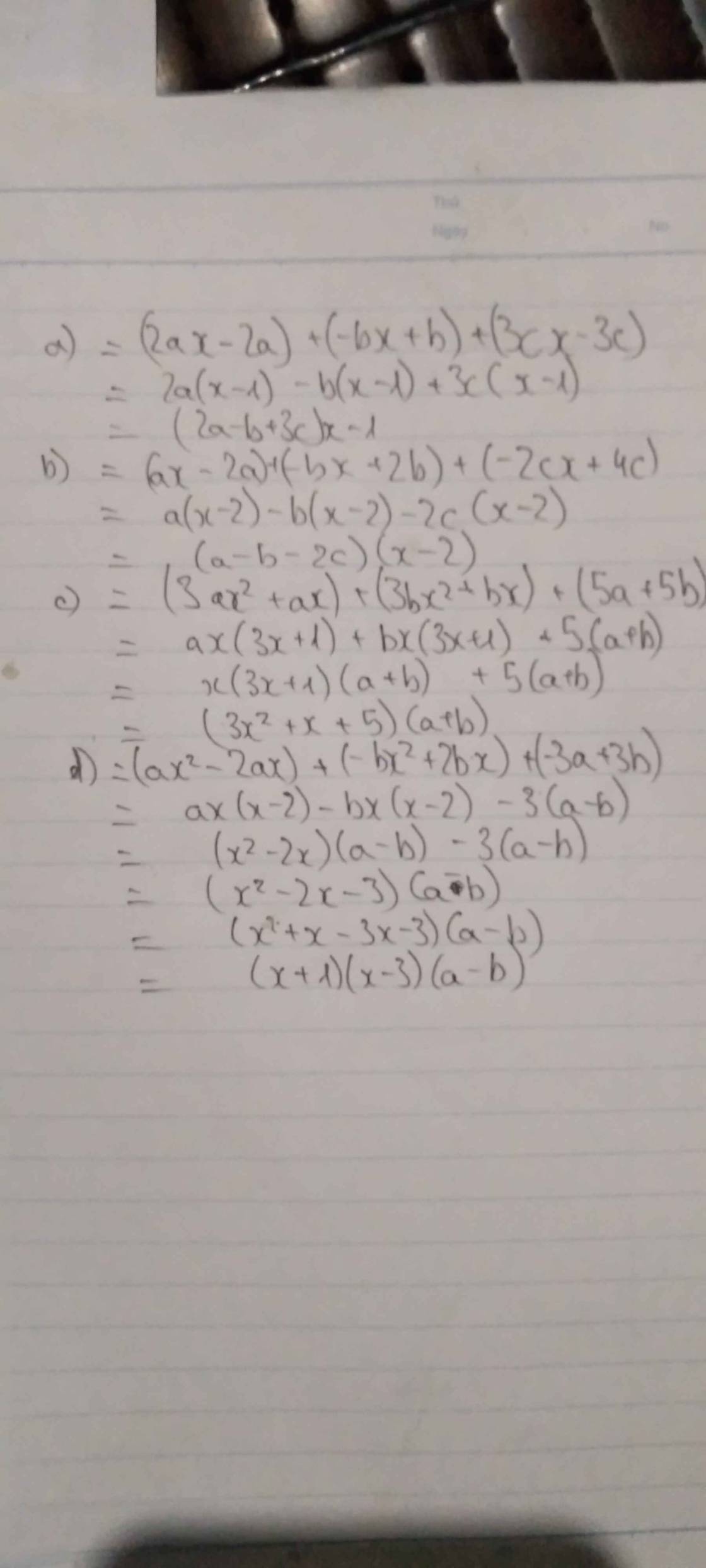Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.\: 2a^2b\left(x+y\right)-4a^3b\left(-x-y\right)\\ =\left(x+y\right)\left(2a^2b+4a^3b\right)\\ =2a^2b\left(x+y\right)\left(1+2a\right)\)
\(b.\:-3a\left(x-y\right)-a^2\left(7-x\right)\\ =a\left(3y-3x-7a+ax\right)\)

a, x(a - b) + (a - b)
= (x + 1)(a - b)
b, x(a + b) - a - b
= x(a + b) - (a + b)
= (x - 1)(a + b)
c, 10ax - 5ay - 2x + y
= 5a(2x - y) - (2x - y)
= (5a - 1)(2x - y)
d, 2a^2x - 5by - 5a^2y + 2bx
= 2x(a^2 + b) - 5y(b + a^2)
= (2a - 5y)(a^2 + b)
làm tiếp:
2ax2 - bx2 - 2ax +bx +4a-2b
= x2(2a-b) - x(2a-b) +2(2a-b)
=(2a-b)(x2-x+2)

\(2ax-bx+3cx-2a+b-3c\\ =x\left(2a-b+3c\right)-\left(2a-b+3c\right)\\ =\left(x-1\right)\left(2a-b+3c\right)\)
\(ax-bx-2cx-2a+2b+4c\\ =x\left(a-b-2c\right)-2\left(a-b-2c\right)\\ =\left(x-2\right)\left(a-b-2c\right)\)
\(3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\)
\(ax^2-bx^2-2ax+2bx-3a+3b\\ =x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a+b\right)\\ =\left(x^2-2x-3\right)\left(a+b\right)\\ =\left(x+1\right)\left(x-3\right)\left(a+b\right)\)

a) \(2a^2x-5by-5a^2y+2by\)
\(=3\left(\frac{2}{3}a^2x-\frac{5}{3}a^2y\right)-3by\)
\(=3\left(\frac{2}{3}a^2x-\frac{5}{3}a^2y-by\right)\)

a) \(\left(x+y\right)^3-x^3-y^3\)
\(=\left(x+y\right)^3-\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=\left(x+y\right)\left[\left(x+y\right)^2-x^2+xy-y^2\right]\)
\(=\left(x+y\right)\left(x^2+2xy+y^2-x^2+xy-y^2\right)\)
\(=3xy\left(x+y\right)\)
b) \(x^2+y^2+2xy+yz+xz\)
\(=\left(x^2+2xy+y^2\right)+\left(yz+xz\right)\)
\(=\left(x+y\right)^2+z\left(x+y\right)\)
\(=\left(x+y\right)\left(x+y+z\right)\)
c) \(x^2-10xy-1+25y^2\)
\(=\left(x^2-10xy+25y^2\right)-1\)
\(=\left(x-5y\right)^2-1\)
\(=\left(x-5y-1\right)\left(x-5y+1\right)\)
d) \(ax^2-ax+bx^2-bx+a+b\)
\(=(ax^2+bx^2)-(ax+bx)+(a+b)\)
\(=x^2(a+b)-x(a+b)+(a+b)\)
\(=(a+b)(x^2-x+1)\)
e)\(x^2-2y+3xz+x-2y+3z\)
\(=(x^2+x)-(2xy+2y)+(3xz+3z)\)
\(=x(x+1)-2y(x-1)+3z(x+1)\)
\(=(x+1)(x-2y+3z)\)
f) \(xyz-xy-yz-xz+x+y+z-1\)
\(=(xyz-xy)-(yz-y)-(xz-x)+(z-1)\)
\(=xy(z-1)-y(z-1)-x(z-1)+(z-1)\)
\(=(z-1)(xy-y-x+1)\)
\(=(z-1)[y(x-1)-(x-1)]\)
\(=(z-1)(x-1)(y-1)\)
_Học tốt_

A = 4acx + 4bcx + 4ax + 4bx ( đã sửa '-' )
= 4x( ac + bc + a + b )
= 4x[ c( a + b ) + ( a + b ) ]
= 4x( a + b )( c + 1 )
B = ax - bx + cx - 3a + 3b - 3c
= x( a - b + c ) - 3( a - b + c )
= ( a - b + c )( x - 3 )
C = 2ax - bx + 3cx - 2a + b - 3c
= x( 2a - b + 3c ) - ( 2a - b + 3c )
= ( 2a - b + 3c )( x - 1 )
D = ax - bx - 2cx - 2a + 2b + 4c
= x( a - b - 2c ) - 2( a - b - 2c )
= ( a - b - 2c )( x - 2 )
E = 3ax2 + 3bx2 + ax + bx + 5a + 5b
= 3x2( a + b ) + x( a + b ) + 5( a + b )
= ( a + b )( 3x2 + x + 5 )
F = ax2 - bx2 - 2ax + 2bx - 3a + 3b
= x2( a - b ) - 2x( a - b ) - 3( a - b )
= ( a - b )( x2 - 2x - 3 )
= ( a - b )( x2 + x - 3x - 3 )
= ( a - b )[ x( x + 1 ) - 3( x + 1 ) ]
= ( a - b )( x + 1 )( x - 3 )