Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2x^2y^3-\frac{x}{4}-4y^6\)
đây là pt bậc 2 của y^3 , ta đặt y^3=z ta được
\(-\left(4z^2+\frac{2.2xz}{2}+\frac{x^2}{4}\right)+\left(\frac{x^2}{4}-\frac{x}{4}\right)\)
\(-\left(2z+\frac{x}{2}\right)^2+\left(\frac{x^2}{4}-\frac{x}{4}\right)\)
\(-\left\{\left(2x+\frac{x}{2}\right)^2-\left(\frac{x^2}{4}-\frac{x}{4}\right)\right\}\)
\(-\left\{\left(2x+\frac{x}{2}+\sqrt{\frac{x^2}{4}-\frac{x}{4}}\right)\left(2x+\frac{x}{2}-\sqrt{\frac{x^2}{4}-\frac{x}{4}}\right)\right\}\)

a) \(\left(2x+5\right)^2\)\(-\left(x-9\right)^2\)
=\(\left(2x+5+x-9\right).\left(2x+5-x+9\right)\)
=\(\left(3x-4\right).\left(x+14\right)\)

b) \(64x^3+1=\left(4x+1\right)\left(16x^2-4x+1\right)\)\
c) \(x^3y^6z^9-125=\left(xy^2z^3-5\right)\left(x^2y^4z^6+5xy^2z+25\right)\)
d) \(27x^6-8x^3=x^3\left(27x^3-8\right)=x^3\left(3x-2\right)\left(9x^2+6x+4\right)\)
e) \(x^6-y^6=\left(x^3-y^3\right)\left(x^3+y^3\right)=\left(x-y\right)\left(x^2+xy+y^2\right)\left(x+y\right)\left(x^2-xy+y^2\right)\)

64x3 + 1
= ( 4x )3 + 1
= ( 4x + 1 ) ( 16x2 - 4x + 1 )
Hằng đẳng thức 6 : A3 + B3
27x6 - 8x3
= ( 3x2)3 + ( 2x )3
= ( 3x + 2x ) ( 9x2 - 6x + 4x2 )
HĐT 6

x6 - y6
= ( x2 )3 - ( y2 )3
= ( x2 - y2 ) ( x4 + x2y2 + y4 )
HĐT 7 : A3 - B3
x3y6z9 + 1
= ( xy2z3)3 + 1
= ( xy2z3 + 1 ) ( x2y4z6 + zy2z3 + 1 )
HĐT 6

a: \(x^3-2x+4\)
\(=x^3+2x^2-2x^2-4x+2x+4\)
\(=\left(x+2\right)\left(x^2-2x+2\right)\)
b: \(x^3-4x^2+12x-27\)
\(=\left(x-3\right)\left(x^2+3x+9\right)-4x\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-x+9\right)\)
c: \(x^3+2x^2+2x+1\)
\(=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+1\right)\)

\(2x^2-7x+3\)
\(=2\left(x^2-\frac{7}{2}x+\frac{3}{2}\right)\)
Vậy thôi đâu cần dùng HĐT

Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)
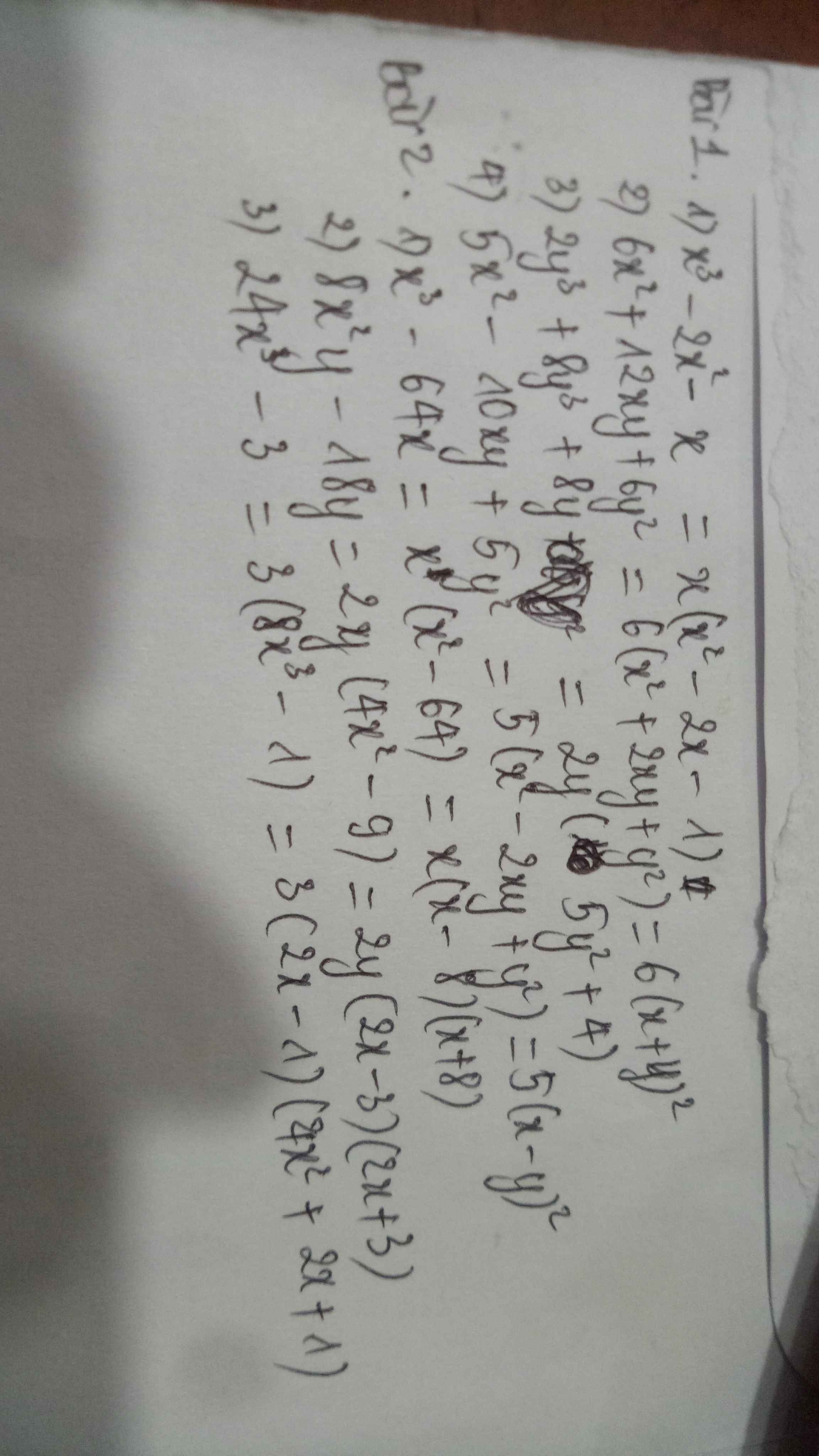
4: \(\left(2x+3\right)^3-1\)
\(=\left(2x+3-1\right)\left(4x^2+12x+9+2x+3+1\right)\)
\(=\left(2x+2\right)\left(4x^2+14x+13\right)\)
\(=2\left(x+1\right)\left(4x^2+14x+13\right)\)
5: \(4x^2+20xy+25y^2=\left(2x+5y\right)^2\)
6: \(x^4-64xy^3\)
\(=x\left(x^3-64y^3\right)\)
\(=x\left(x-4y\right)\left(x^2+4xy+16y^2\right)\)