NP
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NC
4
S
27 tháng 10 2014
Đặt x2+x+1=t
Ta có: t(t+1)-12 = t2+t-12 = t2+4t-3t-12 = t(t+4) -3(t+4) =(t-3)(t+4) = (x2+x+1-3)(x2+x+1+4) =(x2+x-2)(x2+x+5).
NN
2
D
24 tháng 7 2017
(x2+x+1)(x2+x+2)-12
=\(\left(x^2+x+\frac{3}{2}-\frac{1}{2}\right)\left(x^2+x+\frac{3}{2}+\frac{1}{2}\right)-12\)
=\(\left(x^2+x+\frac{3}{2}\right)^2-\frac{1}{4}-12\)
=\(\left(x^2+x+\frac{3}{2}\right)^2-\frac{49}{4}\)
=\(\left(x^2+x+\frac{3}{2}-\frac{7}{2}\right)\left(x^2+x+\frac{3}{2}+\frac{7}{2}\right)\)
=\(\left(x^2+x-2\right)\left(x^2+x+5\right)\)
KT
21 tháng 10 2018
\(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt: \(x^2+x+1=t\) Khi đó ta có:
\(A=t\left(t+1\right)-12\)
\(=t^2+t-12=\left(t-3\right)\left(t+4\right)\)
Thay trở lại đc:
\(A=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
LC
3
MT
10 tháng 10 2015
(x2+x+1)(x2+x+2)-12
=(x2+x+1)[(x2+x+1)+1)-12
=(x2+x+1)2+(x2+x+1)-12
=(x2+x+1)2-3.(x2+x+1)+4.(x2+x+1)-12
=(x2+x+1)(x2+x+1-3)+4.(x2+x+1-3)
=(x2+x+1)(x2+x-2)+4.(x2+x-2)
=(x2+x-2)(x2+x+1+4)
=(x2-x+2x-2)(x2+x+5)
=[x.(x-1)+2.(x-1)](x2+x+5)
=(x-1)(x+2)(x2+x+5)
4 tháng 3 2017
(x^2+x+1)(x^2+x+2)-12
Đặt x^2+x+1= a ta có
=a^2+a-12
=a^2-3a+4a-12
=(a^2-3a)+(4a-12)
=a(a-3)+4(a-3)
=(a-3)(a+4)
thay x^2+x+1=a ta được
(x^2+x-2)(x^2+x+5)
PM
1
22 tháng 8 2016
Đặt : u=x2+x+1
Ta có : u(u+1)-12
=u2+u-12
=u2+4u-3u-12
=u(u+4)-3(u+4)
=(u+4)(u-3)
=(x2+x+1+4)(x2+x+1-3)
=(x2+x+5)(x2+x-2)
=(x2+x+5)[(x2+2x)-x-2]
=(x2+x+5)[(x2+2x)-(x+2)]
=(x2+x+5)(x+2)(x-1)
Nhận xét : x2+x+5>0 , với mọi x , nên không phân tích được nữa
PT
2
12 tháng 8 2015
Đặt x^2 + x+ 1 = a => x^2 + x + 2 =a + 1
Thay vòa ta có :
a( a+ 1 ) - 12 = a^2 + a - 12 = a^2 + 4a - 3a - 12
=a (a+4) - 3 ( a+ 4 )
= ( a- 3 )(a+4)
Thây x^2 + x + 1 = a vào ta có
(x^2 + x + 1 - 3 )(x^2 + x + 1 + 4 )
= ( x^2 + x - 2 )( x^ 2 + x + 5 )
MT
12 tháng 8 2015
đặt t=x2+x+1 ta được:
t.(t+1)-12
=t2-t-12
=t2+3x-4t-12
=t.(t+3)-4.(t+3)
=(t+3)(t-4)
thay t=x2+x+1 ta được:
(x2+x+4)(x2+x-3)
vậy (x2 + x + 1) . (x2 + x + 2) - 12=(x2+x+4)(x2+x-3)
TT
1
21 tháng 8 2015
Đặt x^2 + x +1 = a
Thay vào ta có :
a(a+1) - 12
= a^2 + a - 12
= a^2 + 4a - 3a - 12
= a(a+4 ) - 3 (a + 4 )
=(a- 3 )(a+4 )
Thay a = x^2 + x + 1 ta có :
= ( x^2 + x + 1 - 3 )(x^2 + x + 1 + 4 )
=(x^2 + x - 2 )(x^2 + x + 5 )
VA
0
A
2
29 tháng 8 2019
Đặt \(x^2-3x-1=a\)thay vào biểu thức ta được :
\(a^2-12a+27\)
\(=a^2-3a-9a+27\)
\(=a\left(a-3\right)-9\left(a-3\right)\)
\(=\left(a-3\right)\left(a-9\right)\)(1)
Thay \(a=x^2-3x-1\)vào (1) ta được :
\(\left(x^2-3x-1-3\right)\left(x^2-3x-1-10\right)\)
\(=\left(x^2-3x-4\right)\left(x^2-3x-11\right)\)
2 tháng 10 2019
Bạn Châu sai đáp án cuối
phải là (x2-3x-4)(x2-3x-10) nha
LP
2
MH
31 tháng 7 2015
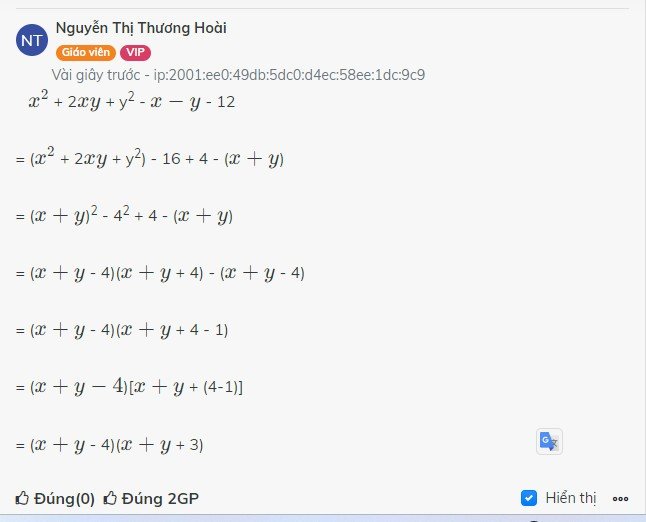
x2+2xy+y2-x-y-12
= (x+y)2-(x+y)-12
đặt x+y=z. ta có:
z2-z-12
= z2-4z+3z-12
= z(z-4)+3(z-4)
= (z-4)(z+3)
thay x+y=z:
= (x+y-4)(x+y+3)
