Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
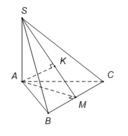
Gọi M là trung điểm BC
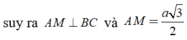
Gọi K là hình chiếu của A trên SM , suy ra AK ⊥ SM. (1)
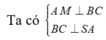
![]()
![]()
![]()
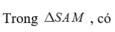
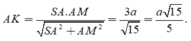
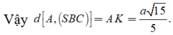

Đáp án C
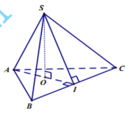
Ta chứng minh được hai mặt phẳng (SAI) (ABC) cùng vuông góc với nhau. Gọi O là hình chiếu của S lên AI
suy ra SO ⊥ (ABC)
Ta có AI =SI = a 3 2 =SA => ∆ S A I đều =>SI = SA . a 3 2 = 3 a 4

Chọn A
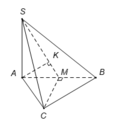
Xác định được
![]()
![]()
Do M là trung điểm của cạnh AB nên
![]()
![]()
![]()
Tam giác vuông SAM có
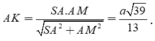
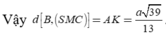

Gọi H là trung điểm AD \(\Rightarrow SH\perp\left(ABCD\right)\) và \(SH=\dfrac{a\sqrt{3}}{2}\)
Gọi M là trung điểm BC \(\Rightarrow HM||CD\Rightarrow HM\perp CB\) đồng thời \(HM=CD=a\)
\(\Rightarrow BC\perp\left(SHM\right)\)
Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SBC\right)\)
\(\Rightarrow HK=d\left(H;\left(SBC\right)\right)\)
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{HM^2}\Rightarrow HK=\dfrac{SH.HM}{\sqrt{SH^2+HM^2}}=\dfrac{a\sqrt{21}}{7}\)
\(DH||BC\Rightarrow DH||\left(SBC\right)\Rightarrow d\left(D;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)=\dfrac{a\sqrt{21}}{7}\)
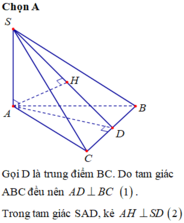

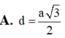
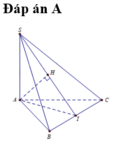

● Gọi M là trung điểm của BC ; H là hình chiếu vuông góc của A trên SM.
● Vì tam giác ABC đều nên: BC ⊥ AM.
- Trong tam giác vuông SAM, đường cao AH có: