Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Xét điểm C bất kỳ dao động với biên độ cực đại trên Ax ta có:
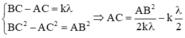
M là điểm xa nhất ta lấy
![]()
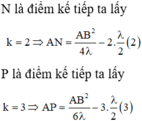
Từ (1), (2), (3) ta tìm được λ = 4cm và AB = 18cm. Lập tỉ số
AB
λ
=4,5; Điểm Q gần A nhất ứng với k = 4 ta có: 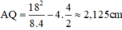

Đáp án C
Theo bài ra M là điểm xa A nhất nên M thuộc cực tiểu thứ 1, N thuộc cực tiểu thứ 2, P thuộc cực tiểu thứ 3. Vì hai nguồn ngược pha nên ta có:
M B − M A = λ N B − N A = 2 λ P B − P A = 3 λ ⇒ a 2 + m + 22 , 75 + 8 , 75 2 − m + 22 , 25 + 8 , 75 = λ a 2 + m + 8 , 75 2 − m + 8 , 75 = 2 λ a 2 + m 2 − m = 3 λ
Trong đó: A B = a ; A P = m . Ta có:
a 2 = λ 2 + 2 λ m + 31 a 2 = 4 λ 2 + 4 λ m + 8 , 75 a 2 = 9 λ 2 + 6 λ m nên 4 λ 2 + 4 λ m + 8 , 75 − λ 2 − 2 λ m + 31 = 0 9 λ 2 + 6 λ m = a 2
⇒ 3 λ 2 + 2 λ m = 27 λ 9 λ 2 + 6 λ m = a 2 ⇒ 27 λ = a 2 3 ⇒ a 2 = 81 λ ⇒ a = 18 λ = 4 m = 7 , 5
Vì Q thuộc Ax và gần A nhất nên Q phải thuộc cực tiểu thứ 4
Nên Q B − Q A = 4 λ ⇒ a 2 + Q A 2 − Q A = 4 λ
⇒ 18 2 + Q A 2 − Q A = 4.4 ⇒ Q A = 2 , 125 c m

Đáp án C
Theo bài ra M là điểm xa A nhất nên M thuộc cực tiểu thứ 1, N thuộc cực tiểu thứ 2, P thuộc cực tiểu thứ 3. Vì hai nguồn ngược pha nên ta có:

Trong đó: AB = a, AP = m. Ta có:
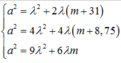 nên
nên

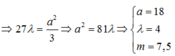
Vì Q thuộc Ax và gần A nhất nên Q phải thuộc cực tiểu thứ 4.
Nên
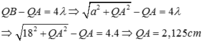

Chọn C
+ Khoảng cách giữa hai cực đại liên tiếp trên AB là 0,5l
+ Vì trên AB có 14 cực đại nên: 7 λ < A B = a ≤ 8 λ
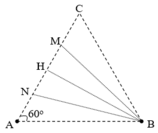
+ Gọi N và M là hai điểm cực đại cùng pha liên tiếp trên AC
Điều kiện cực đại liên tiếp:
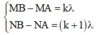
Þ NB – MB + MA – NA = l Û NB – MB + MN = l (1)
Điều kiện cùng pha liên tiếp:
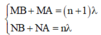
Þ MB – NB + MA – NA = l Û MB – NB + MN = l (2)
Từ (1) và (2) suy ra NB = MB Þ MN = l
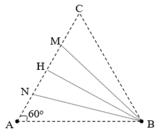
+ Gọi H là trung điểm của NM Þ BH ^ AH Þ BH là đường cao trong tam giác đều hạ từ B đến AC. Ta có:
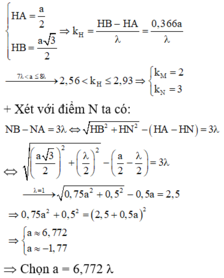

Đáp án D
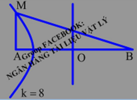
Bước sóng: λ = v f = 40 20 = 2 c m
Vì hai nguồn ngược pha nên điều kiện cực đại cho M là: M A − M B = k + 0 , 5 λ = 2 k + 1
Vì M gần A nhất nên M phải thuộc cực đại ngoài cùng về phía A.
Số cực đại trên AB: − A B λ − 1 2 < k < A B λ − 1 2
⇒ − 8 , 5 < k < 8 , 5 ⇒ k = − 8 ⇒ M A − M B = 2 − 8 + 1 = − 15 ⇒ M B = M A + 15 1
Vì Δ A M B vuông tại A nên: M A 2 + A B 2 = M B 2 2
Thay (1) vào (2) ta có: M A 2 + 16 2 = M A + 15 2 ⇒ M A = 1 , 03 c m
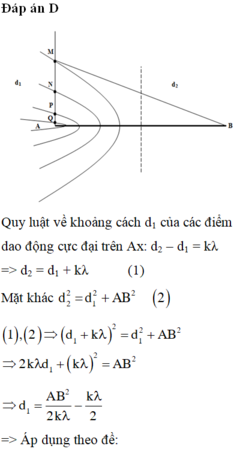
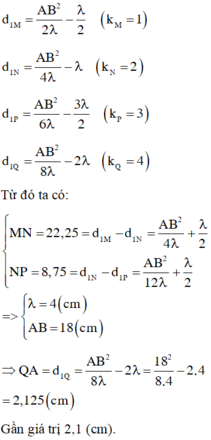


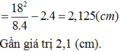



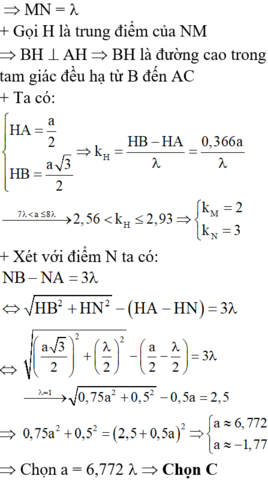
Ta thấy trên nửa đường thẳng thẳng kẻ từ A và vuông góc với AB có 4 điểm theo thứ tự M, N, P, Q dao động với biên độ cực đại, nên trên AB có 9 điểm dao động với biên độ cực đai với - 4 ≤ k ≤ 4 ( d2 – d1 = kλ)
A B x M N P Q
Cực đại tại M, N, P, Q ứng với k = 1; 2; 3; 4
Đặt AB = a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB – CA = kλ (*)
CB2 – CA2 = a2 → (CB + CA) (CB – CA) = a2
CB + CA = \(\dfrac{a^2}{k.\lambda}\)(**)
Từ (*) và (**) suy ra \(CA=\dfrac{a^2}{2k.\lambda}-\dfrac{k}{2}\lambda\)
Tại M: ứng với k = 1: MA = \(\dfrac{a^2}{2\lambda}\)- 0,5λ (1)
Tại N: ứng với k = 2: NA = \(\dfrac{a^2}{4\lambda}\)- λ (2)
Tại P: ứng với k = 3: PA = \(\dfrac{a^2}{6\lambda}\) - 1,5 λ (3)
Tại Q: ứng với k = 4: QA = \(\dfrac{a^2}{8\lambda}\) - 2 λ (4)
Lấy (1) – (2) : MN = MA – NA = \(\dfrac{a^2}{4\lambda}\) + 0,5λ = 22,25 cm (5)
Lấy (2) – (3) : NP = NA – PA = \(\dfrac{a^2}{12\lambda}\) + 0,5λ = 8,75 cm (6)
Lấy (5) - (6) → \(\dfrac{a^2}{\lambda}\) = 81 (cm) và λ = 4 cm .
Thế vào (4) → QA = 2,125 cm.
thầy có thể giải thích e chổ CB-CA= Klamda . Với tại s CB= K/2 lamda k thầy?