Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Bước sóng của sóng :
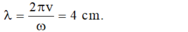
→ Khi xảy ra hiện tượng giao thoa sóng nước với hai nguồn kết hợp ngược pha. Trung điểm I của đoạn thẳng nối hai nguồn là một cực tiểu giao thoa (có thể xem gần đúng là một nút như hiện tượng sóng dừng).
→ Biên độ dao động của điểm M cách bụng I một đoạn d là:
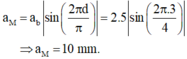

Bước sóng của sóng
Khi xảy ra hiện tượng giao thoa sóng nước với hai nguồn kết hợp ngược pha. Trung điểm I của đoạn thẳng nối hai nguồn là một cực tiểu giao thoa (có thể xem gần đúng là một nút như hiện tượng sóng dừng).
Biên độ dao động của điểm M cách bụng I một đoạn d là: a M = a b sin 2 πd π = 2 . 5 sin 2 π 3 4 = 10 mm
Chọn đáp án C

Đáp án C
+ Bước sóng của sóng λ = 2 πv ω = 4 cm .
→ Khi xảy ra hiện tượng giao thoa sóng nước với hai nguồn kết hợp ngược pha. Trung điểm I của đoạn thẳng nối hai nguồn là một cực tiểu giao thoa (có thể xem gần đúng là một nút như hiện tượng sóng dừng).
→ Biên độ dao động của điểm M cách bụng I một đoạn d là:
a M = a b sin ( 2 πd π ) = 2 . 5 sin ( 2 π . 3 4 ) = 10 mm .

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Chọn C
λ = v f = 4 c m
Hai nguồn dao động ngược pha nhau nên
- 20 < ( k + 0 , 5 ) λ < 20 → - 20 < ( k + 0 , 5 ) · 4 < 20
có 10 giá trị k thỏa mãn

Đáp án C
+ Bước sóng của sóng λ = 2 πv ω = 2 π . 80 40 π = 4 cm .
=> Số điểm dao động với biên độ cực đại
- S 1 S 2 λ - 1 2 ≤ k ≤ S 1 S 2 λ - 1 2 → - 6 , 75 ≤ k ≤ 5 , 5
=> Có 12 điểm dao động với biên độ cực đại.

Chọn C
+ Bước sóng của sóng λ = v 2 π ω = 3 , 5 c m
Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:
- A B λ ≤ k ≤ A B λ ⇔ - 5 , 7 ≤ k ≤ 5 , 7
Vậy có 11 điểm
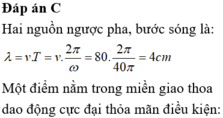
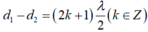
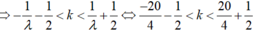
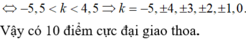
\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)
A