Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ bài tập 2 trang 57 Sách giáo khoa Toán 8 – Cánh diều ta có kết quả: Đường thẳng song song với hai đáy của hình thang thì định ra trên hai cạnh bên các đoạn thẳng tỉ lệ.
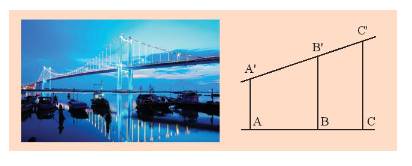
Do các thanh AA’, BB’, CC’, DD’ của giàn gỗ song song với nhau nên ta có các hình thang ACC’A’, BDD’B’.
Xét hình thang ACC’A’ với BB’ song song với hai đáy AA’ và CC’, ta có:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\,\,\left( 1 \right)\)
Xét hình thang BDD’B’ với CC’ song song với hai đáy BB’ và DD’, ta có:
\(\frac{{BC}}{{CD}} = \frac{{B'C'}}{{C'D'}} \Rightarrow \frac{{BC}}{{B'C'}} = \frac{{CD}}{{C'D'}}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CD}}{{C'D'}}\)
Vậy độ dài các đoạn AB, BC, CD lần lượt tỉ lệ với độ dài các đoạn A’B’, B’C’, C’D’.

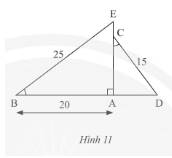
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)

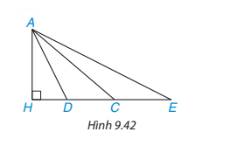
Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có: \(A{{\rm{D}}^2} = A{H^2} + H{{\rm{D}}^2}\) (1)
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có: \(A{C^2} = A{H^2} + H{C^2}\) (2)
Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có: \(A{E^2} = A{H^2} + H{E^2}\) (3)
Vì HE > HC > HD suy ra \(H{E^2} > H{C^2} > H{{\rm{D}}^2}\)(4)
Từ (1), (2), (3), (4) suy ra: \(A{{\rm{E}}^2} > A{C^2} > A{{\rm{D}}^2} \Rightarrow A{\rm{E}} > AC > A{\rm{D}}\)
Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.

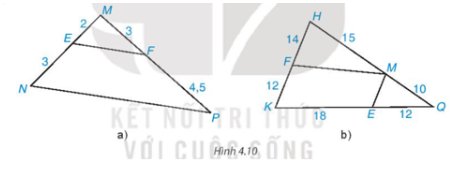
• Hình 4.10a)
Ta có: \(\dfrac{{EM}}{{EN}} = \dfrac{2}{3};\dfrac{{MF}}{{PF}} = \dfrac{3}{{4,5}} = \dfrac{2}{3}\) nên \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\)
Vì \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\), E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: \(\dfrac{{HF}}{{KF}} = \dfrac{{14}}{{12}} = \dfrac{7}{6};\dfrac{{HM}}{{MQ}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)
Vì \(\dfrac{{HF}}{{KF}} \ne \dfrac{{HM}}{{MQ}}\) nên MF không song song với KQ.
* Ta có: \(\dfrac{{MQ}}{{MH}} = \dfrac{{10}}{{15}} = \dfrac{2}{3};\dfrac{{EQ}}{{EK}} = \dfrac{{12}}{{18}} = \dfrac{2}{3}\)
Vì \(\dfrac{{MQ}}{{MH}} = \dfrac{{EQ}}{{EK}}\); F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.

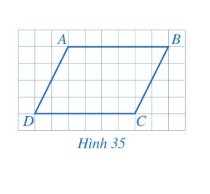
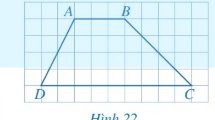
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow B'C' = \frac{{BC.A'B'}}{{AB}}\).