Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Nhiệt độ ban đầu là:
\(T=25+70\cdot e^{-0.5\cdot0}=95\left(^0C\right)\)
b: ĐặtT=30
=>\(25+70\cdot e^{-0.5t}=30\)
=>\(e^{-0.5t}=\dfrac{1}{14}\)
=>\(-0.5t=ln\left(\dfrac{1}{14}\right)\)
=>\(t\simeq5,28\simeq6\)
=>Sau 6 phút thì nhiệt độ còn lại tầm 30 độ C

\(\begin{array}{l} - 1 \le sin\frac{\pi }{{12}}(t - 9)\; \le 1\\ \Leftrightarrow - 3 \le 3sin\frac{\pi }{{12}}(t - 9)\; \le 3\\ \Leftrightarrow - 26 \le 29 + 3sin\frac{\pi }{{12}}(t - 9)\; \le 32\\ \Leftrightarrow - 26 \le h(t) \le 32\end{array}\)
Vâỵ nhiệt độ thấp nhất trong ngày là 26°C khi:
\(\begin{array}{l}29 + 3sin\frac{\pi }{{12}}(t - 9) = 26\\ \Leftrightarrow sin\frac{\pi }{{12}}(t - 9) = - 1\\ \Leftrightarrow \frac{\pi }{{12}}(t - 9) = - \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 3 + 24k,k \in \mathbb{Z}.\end{array}\)
Do t là thời gian trong ngày tính bằng giờ nên \(0 \le t \le 24\). Suy ra: \(k = 0 \Rightarrow t = 3\).
Vì vậy vào thời điểm 3 giờ trong ngày thì nhiều độ thấp nhất của thành phố là 26°C.
Đáp án: C

Mấy câu trả lời SGK trình bày giúp anh Latex cái hoặc gõ ra nhưng gõ định dạng ấy em. Chứ như thế này anh sợ nhiều người không đọc được chữ ấy, mặc dù anh cũng đọc được.
Ta có:
\(\begin{array}{l}P'\left( t \right) = \frac{{{{\left( {500t} \right)}^\prime }\left( {{t^2} + 9} \right) - \left( {500t} \right){{\left( {{t^2} + 9} \right)}^\prime }}}{{{{\left( {{t^2} + 9} \right)}^2}}}\\ = \frac{{500\left( {{t^2} + 9} \right) - \left( {500t} \right).2t}}{{{{\left( {{t^2} + 9} \right)}^2}}}\\ = \frac{{500{t^2} + 4500 - 1000{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}} = \frac{{4500 - 500{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}}\end{array}\)
Tốc độ tăng dân số tại thời điểm \(t = 12\) là: \(P'\left( {12} \right) = \frac{{4500 - 500{t^2}}}{{{{\left( {{t^2} + 9} \right)}^2}}} \approx - 2,88\).

Ta có: \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right) = 2\left[ {\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right) + \cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)} \right]\)
\(2\left[ {\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} + \frac{\pi }{3}t - \frac{\pi }{3}}}{2}} \right).\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} - \frac{\pi }{3}t + \frac{\pi }{3}}}{2}} \right)} \right] = 2\left[2. {\cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right).\cos \frac{\pi }{4}} \right] = 2\sqrt 2 \cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right)\)
Vậy biên độ là \(2\sqrt 2 \), pha ban đầu \( - \frac{\pi }{{12}}\)

Lời giải:
$\sin (\frac{\pi t}{18}-\frac{\pi}{6})\leq 1$ với mọi $t\in [0;24]$
$\Rightarrow h\leq 2.1+5=7$
Vậy $h_{\max}=7\Leftrightarrow \sin (\frac{\pi t}{18}-\frac{\pi}{6})=1$
$\Leftrightarrow \frac{\pi t}{18}-\frac{\pi}{6})=\frac{\pi}{2}+2k\pi$ với $k$ nguyên
$\Leftrightarrow \frac{t}{18}-\frac{1}{6}=\frac{1}{2}+2k$ với $k$ nguyên
$\Leftrightarrow t=12+36k$ với $k$ nguyên.
Do $t\in [0;24]$ nên $t=12$
Đáp án C.

Hàm số \(T\left( t \right)\) có tập xác định là \(\left[ {0;100} \right]\).
Ta có: \(T\left( {60} \right) = 10 + 2.60 = 130\)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k - 3t} \right) = k - 3.60 = k - 180\\\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}\)
Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm \({t_0} = 60\)
Khi đó: \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k - 180 = 130 \Leftrightarrow k = 310\)
Vậy với \(k = 310\) thì hàm số \(T\left( t \right)\) liên tục trên tập xác định.

a) Biên độ dao động \(A = - 5\); Pha ban đầu của dao động: \(\varphi = 0\)
b) Pha dao động tại thời điểm \(t = 2\) à \(\omega t + \varphi = 4\pi .2 = 8\pi \)
Chu kỳ \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,2\)
Trong khoảng thời gian 2 giây, số dao động toàn phần vật thực hiện được là: \(\frac{2}{{0,2}} = 10\) (dao động)

+) Độ sâu của mực nước là 15m thì h = 15.
Khi đó
\(\begin{array}{l}15 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos 0\\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi - 1} \right)}}{\pi };k \in Z\end{array}\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {k2\pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {2\pi - 1} \right)}}{\pi };\frac{{6\left( {4\pi - 1} \right)}}{\pi }} \right\}\)
+) Độ sâu của mực nước là 9m thì h = 9.
Khi đó
\(\begin{array}{l}9 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = - 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \pi \\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = \pi + k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi + \pi - 1} \right)}}{\pi };k \in Z\end{array}\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {k2\pi + \pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 1\end{array}\)
Lại do \(k \in Z \Rightarrow k = 1 \Rightarrow t = \frac{{6\left( {3\pi - 1} \right)}}{\pi }\)
+) Độ sâu của mực nước là 10,5m thì h = 10,5.
Khi đó
\(\begin{array}{l}10,5 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = - \frac{1}{2}\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \frac{{2\pi }}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{{\pi t}}{6} + 1 = \frac{{2\pi }}{3} + k2\pi \\\frac{{\pi t}}{6} + 1 = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\\t = \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\end{array} \right.\end{array}\)
Với \(t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 \le k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {0;1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {\frac{{2\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{8\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{14\pi }}{3} - 1} \right)}}{\pi }} \right\}\)
Với \(t = \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi };k \in Z\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( { - \frac{{2\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{4\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{10\pi }}{3} - 1} \right)}}{\pi }} \right\}\)

Ta có: \(s\in\left[-1;1\right]\Leftrightarrow-1\le2cos\left(\pi t\right)\le1\\ \Leftrightarrow-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\)
Trong 1s đầu tiên \(0< t< 1\Rightarrow0< \pi t< \pi\)
Ta có đồ thị hàm số \(y=cos\left(x\right)\) trên \(\left[0;\pi\right]\)
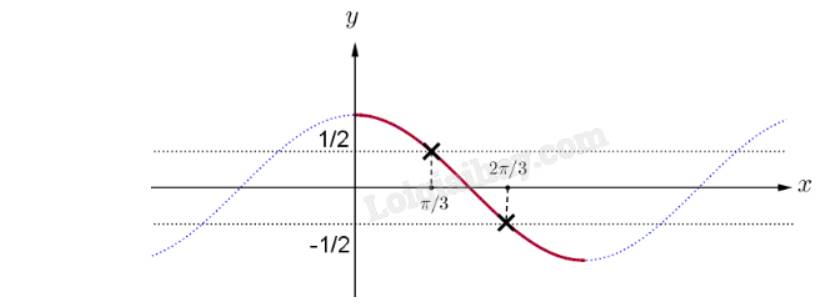
Dựa vào đồ thị, ta thấy
\(-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\Leftrightarrow\dfrac{\pi}{3}\le\pi t\le\dfrac{2\pi}{3}\Leftrightarrow\dfrac{1}{3}\le t\le\dfrac{2}{3}\)
Vậy \(t\in\left[\dfrac{1}{3};\dfrac{2}{3}\right]\)

Ta có:
\(T'\left(t\right)=-0,1\cdot2t+1,2=-0,2t+1,2\)
Tốc độ thay đổi của nhiệt độ ở thời điểm t = 1,5s là:
\(T'\left(1,5\right)=-0,2\cdot1,5+1,2=0,9\)