K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
WH
12 tháng 7 2020
3b/ giải ch ra :(
4/ ko hiểu đề + lười
5/
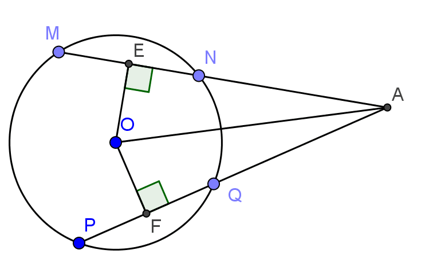
a/ Vì M là tđ AC => OM vuông góc vs AC => ^OMC = 90o
Vì N là tđ BC => ON vuông vs BC => ^ONC = 90o
=> ^OMC = ^ONC = 90o
Mà 2 góc này cùng chắn cung OC
=> tứ giac OCMN nội tiếp
LẠi có : AB = AC (gt) => sđ cung AB = sđ cung AC => ^CDA = ^ADB ( hệ quả góc nội tiếp ) => ^CDB = 2.^CDA
cmtt => ^CDM=^MDA (...) => ^CDA = 2.^MDC
=> ^CDB = 4.^MDC (đpcm)
b,c / ...
11 tháng 7 2020
Lời giải bài hình của mình:
a) +) \(\widehat{ONC}=\widehat{OMC}=90^0\) nên ONMC nội tiếp.
+) \(\widehat{BDC}=2\widehat{ADC}=4\widehat{ODC}\)
b) \(\widehat{PAC}=\frac{1}{2}sđ\stackrel\frown{DC}=\frac{1}{2}sđ\stackrel\frown{DA}=\frac{1}{2}sđ\stackrel\frown{DB}+\frac{1}{2}sđ\stackrel\frown{AB}=\frac{1}{2}sđ\stackrel\frown{DB}+\frac{1}{2}sđ\stackrel\frown{AC}=\widehat{APC}\)
Do đó \(\Delta APC\) cân tại \(C\) \(\Rightarrow CA=CP\)
Từ câu a) suy ra \(\widehat{ADM}=\widehat{EDA}\left(=\frac{1}{8}sđ\stackrel\frown{BC}\right)\)
Tứ giác \(DEMC\) nội tiếp \(\Rightarrow\widehat{BEF}=\widehat{MEC}=\widehat{MDC}=\widehat{BDE}\)
Mà \(\widehat{BDE}+\widehat{EBD}=90^0\Rightarrow EF\perp BD\)
c) \(MN\) là đường trung bình của \(\Delta ABC\Rightarrow MN\text{//}AF\Rightarrow\widehat{EMN}=\widehat{AFE}=\widehat{BEF}=\widehat{MEN}\)
\(\Rightarrow\Delta MNE\) cân tại \(N\)
Ta có: \(\left\{{}\begin{matrix}\widehat{BFD}=\widehat{BED}=90^0\\\widehat{FDB}=\widehat{EDB}\end{matrix}\right.\)
\(\Rightarrow\Delta BFD=\Delta BED\left(ch-gn\right)\Rightarrow DE=DF\Rightarrow\frac{DE}{DF}=1\)
ND
0
đạt giá trị nhỏ nhất khi x = 
T
1
28 tháng 4 2020
\(x^2+x-4+\left(x+6\right).\sqrt{x+2}=0\)
\(x^2+x-4+\left(x+6\right)\sqrt{x+2}=0\)
\(\left(x+6\right)\sqrt{x+2}=-x^2-x+4\)
\(\left(x+6\right)^2\left(x+2\right)=\left(-x^2-x+4\right)^2\)
\(x^3+2x^2+12x^2+24x+36x+72=\left(-x^2-x+4\right)\left(-x^2-x+4\right)\)
\(x^3+14x^2+60x+72=-\left(-x^4-x^3+4x^2\right)-\left(-x^3-x^2+4x\right)-4x^2-4x+16\)
\(x^3+14x^2+60x+72=x^4+x^3-4x^2+x^3+x^2-4x-4x^2-4x+16\)
\(x^3+14x^2+60x+72=x^4+2x^3-7x^2-8x+16\)
\(x^3+14x^2+60x+72-x^4-2x^3+7x^2+8x-16=0\)
\(-x^3+21x^2+68x+56-x^4=0\)
Đến đây chịu chắc phương trình vô nghiệm .
DH
= ....................
1
26 tháng 11 2017
TA CÓ :\(5+2\sqrt{6}=\left(\sqrt{3}+\sqrt{2}\right)^2\)
\(\Rightarrow\frac{\sqrt{5+2\sqrt{6}}}{\sqrt{3}+\sqrt{2}}+2014=\frac{\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}}{\sqrt{3}+\sqrt{2}}+2014\)
\(=1+2014=2015\)
Vậy giá trị biểu thức là 2015.
Thức khuya thế ạ... stress lắm đó nha:((. Nếu mệt quá thì nghỉ ngơi một chút đi ạ, sao không tự thưởng cho bản thân một chút yên bình ạ? Xứng đáng màaa. Anh/chị đừng vì áp lực mà dày vò bản thân đến thế, đau lòng lắm í:<<. Đỗ trường chuyên, nguyện vọng 1 ai cũng lo mà, mình đâu cần phải tiêu cực như thế. Em chưa học lớp 9, cũng chưa đối mặt với nhiều chuyển biến lớn nhưng mà dù có khó khăn đến đâu em cũng mạnh dạn chống lại nó nè. Chúng ta chỉ là những chú chim nhỏ cũng chưa có thể đối đáp với nhiều sóng gió nhưng chúng ta lại cứ việc bay rồi lại rơi xuống, rồi lại bay thêm nữa. Ngại gì một chút khó khăn mà làm dừng bước ta lại, cơ hội là lần thi vào 10 này anh/chị hãy tỏa sáng nhé, em sẽ luôn mong anh/ chị đỗ nguyện vọng 1 nè. Có lẽ em không biết anh/chị là ai nhưng em sẵn lòng chia sẻ những điều vui tươi nè dù chỉ là một chút thôi... Nhưng mà cũng rất ý nghĩa mà phải không. Em thấy trên hoc24 anh/chị rất giỏi còn gì, em không biết hết cuộc sống của anh/chị áp lực như thế nào, khó khăn như tế nào:(( nhưng em mong là anh/chị sẽ giữ gìn sức khỏe học tập thật tốt nhé<3. Mà cho dù có chuyện gì đi nữa thì hãy nhớ việc anh/chị đã cố gắng là sự thật, và sự thật đó sẽ tồn tại mãi mãi đóoo:33
đó h học ngu, học dưới quê th h bame kêu đi lên trường chuyên, đó h bạn học thêm cs kiến thức quá tr còn h mình (1 đứa chx bt mùi học thêm là gì) mới app lực nè=)