
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(f_1\left(x\right)=3e^{2x+1};f_2\left(x\right)=\frac{1}{\cos^{2\left(\frac{\Pi x}{4}\right)}}\) . Khi đó \(f\left(x\right)=f_1\left(x\right)+f_2\left(x\right)\)
- Tìm một nguyên hàm của \(f_1\left(x\right)=3e^{2x+1}\) vì nguyên hàm của hàm số \(e^x\) là hàm số \(e^x\) nên theo quy tắc : "Nếu F(x) là một nguyên hàm của hàm số \(f\left(x\right)\) thì \(F\left(y\left(t\right)\right)\) là một nguyên hàm của hàm số \(f\left(y\left(t\right)\right).y't\) trong đó ta giả thiết rằng các hàm số \(f\left(y\left(t\right)\right).y't\) và \(F\left(y\left(t\right)\right)\) đều được xác định. Đặc biệt là nếu \(y\left(t\right)=at+b,a\ne0\) vafneeus F(x) là một nguyên hàm đối với hàm \(f\left(x\right)\) thì \(\frac{1}{a}F\left(at+b\right)\) là một nguyên hàm đối với hàm số \(f\left(at+b\right)\)" (a)
Nguyên hàm của hàm số \(e^{2x+1}\) là \(F_1\left(x\right)=\frac{1}{2}e^{2x+1}\)
Theo quy tắc "Nếu \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) thì \(kF\left(x\right)\) là một nguyên hàm của hàm số \(kf\left(x\right)\)" (b)
một nguyên hàm của \(3e^{2x+1}\) là hàm số \(3.\frac{1}{2}e^{2x+1}=\frac{3}{2}e^{2x+1}\)
Tìm một nguyên hàm của \(f_2\left(x\right)=\frac{1}{\cos^{2\left(\frac{\Pi x}{4}\right)}}\). Vì hàm số \(\tan x\) là một nguyên hàm của \(\frac{1}{\cos^2x}\) nên theo quy tắc (a) ta có \(\frac{4}{\Pi}\tan\frac{\Pi x}{4}\) là nguyên hàm của \(\frac{1}{\cos^{2\left(\frac{\Pi x}{4}\right)}}\)
Bây giờ áp dụng quy tắc "Nếu F(x) là một nguyên hàm của hàm f(x) và G(x) là một nguyên hàm của hàm số g(x) thì hàm số F(x) + G (x) là môt nguyên hàm của hàm số f(x)+g(x)" (c)
ta thu được \(\frac{3}{2}e^{2x+1}+\frac{4}{\Pi}\) là nguyên hàm của hàm số \(f\left(x\right)\)
Mọi nguyên hàm của \(f\left(x\right)\) được biểu diễn bởi công thức :
\(F\left(x\right)=\frac{3}{2}e^{2x+1}+\frac{4}{\Pi}\tan\left(\frac{\Pi x}{4}\right)+C\)

Biến đổi :
\(4\sin^2x+1=5\sin^2x+\cos^2x=\left(a\sin x+b\cos x\right)\left(\sqrt{3}\sin x+\cos x\right)+c\left(\sin^2x+\cos^2x\right)\)
\(=\left(a\sqrt{3}+c\right)\sin^2x+\left(a+b\sqrt{3}\right)\sin x.\cos x+\left(b+c\right)\cos^2x\)
Đồng nhấtheej số hai tử số
\(\begin{cases}a\sqrt{3}+c=5\\a+b\sqrt{3}=0\\b+c=1\end{cases}\)
\(\Leftrightarrow\) \(\begin{cases}a=\sqrt{3}\\b=-1\\c=2\end{cases}\)

a) Điều kiện x>0. Thực hiện chia tử cho mẫu ta được:
f(x) = =
=
∫f(x)dx = ∫()dx =
+C
b) Ta có f(x) = =
-e-x
; do đó nguyên hàm của f(x) là:
F(x)= =
=
+ C
c) Ta có f(x) =
hoặc f(x) =
Do đó nguyên hàm của f(x) là F(x)= -2cot2x + C
d) Áp dụng công thức biến tích thành tổng:
f(x) =sin5xcos3x = (sin8x +sin2x).
Vậy nguyên hàm của hàm số f(x) là F(x) = -(
cos8x + cos2x) +C
e) ta có
vậy nguyên hàm của hàm số f(x) là F(x) = tanx - x + C
g) Ta có ∫e3-2xdx= -∫e3-2xd(3-2x)= -
e3-2x +C
h) Ta có :
= =

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).

Một trong các nguyên hàm của hàm số \(f\left(x\right)=\cos x+\sin x\) là hàm số \(\sin x-\cos x\) . Từ định lí nếu hàm số f(x) có nguyên hàm F(x) trên khoảng (a,b) thì trên khoảng đó nó có vô số nguyên hàm và hai nguyên hàm bất kì của cùng một hàm cho trên khoảng (a,b) là sai khác nhau một hằng số cộng. suy ra mọi nguyên hàm số đã cho đều có dạng \(F\left(x\right)=\sin x-\cos x+C\), trong đó C là hằng số nào đó.
Để xác định hằng số C ta sử dụng điều kiện F(0)=1
Từ điều kiện này và biểu thức F(x) ta có :
\(\sin0-\cos0+C=1\Rightarrow C=1+\cos0=2\)
Do đó hàm số \(F\left(x\right)=\sin x-\cos x+2\) là nguyên hàm cần tìm
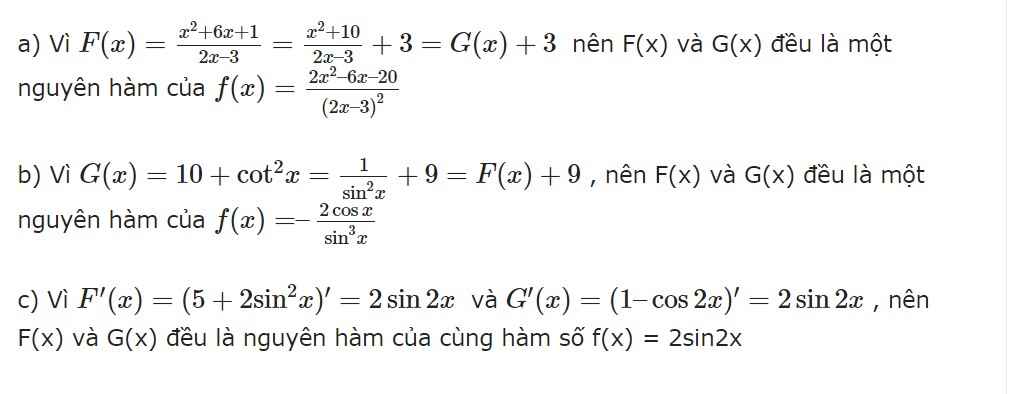



ta có công thức : \(\int a^xdx=\dfrac{a^x}{ina}+C\) \(\Rightarrow\) \(\int2^xdx=\dfrac{2^x}{in2}+C\)
vậy ...