Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Nhiệt độ của chì nay sau khi có sự cân bằng nhiệt là 40 độ C.
2. Nhiệt lượng nước thu vào là \(Q=C_{nước}.m_{nước}.\Delta t=4200.0,4.\left(40-30\right)=16800J.\)
3. Nhiệt lượng chì tỏa ra bằng nhiệt lượng nước thu vào tức là
\(Q_{tỏa}=Q_{thu}\)
=> \(C_{chì}.m_{chì}.\Delta t_2=16800\)
=> \(C_{chì}=\frac{16800}{1,25.80}=168\frac{J}{Kg.K}\)
1) nhiệt độ chì cân bằng là 40
2) nhiệt lượng nước là 16800
3) nhiệt dung riêng chì 168

a) Nhiệt lượng thu vào của nước: Q = mcΔt = 4200.0,25.1,5 = 1575 J
b) Tính nhiệt dung riêng của chì:
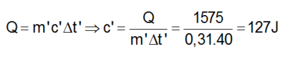
c) So với giá trị ghi ở bảng nhiệt dung riêng thì giá trị này bé hơn là do trong thí nghiệm, một lượng nhỏ nhiệt đã mất mát.

Tóm tắt
\(m_1=300g=0,3kg\\ t_1=100^0C\\ V=0,25l\Rightarrow m_2=0,25kg\\ t_2=58,5^0C\\ t=60^0C\\ \Rightarrow\Delta t_1=t_1-t=100-60=40^0C\\ \Rightarrow\Delta t_2=t-t_2=60-58,5=1,5^0C\\ c_2=4200J/kg.K\)
_____________
\(a.Q_2=?J\\ b.c_1=?J/kg.K\)
Giải
a. Nhiệt lượng nước thu được là:
\(Q_2=m_2.c_2.\Delta t_2=0,25.4200.1,5=1575J\)
b. Nhiệt dung riêng của chì là:
Theo phương trình cân bằng nhiệt:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_1.c_1.\Delta t_1\\ \Leftrightarrow0,3.c_1.40=0,25.4200.1,5\\ \Leftrightarrow12c_1=1575\\ \Leftrightarrow131,25J/kg.K\)
c. Vì nhiệt dung riêng của vật phụ thuộc vào nhiều yếu tố nên có thể cao hoặc thấp nên kết quả tính được chỉ gần đúng giá trị ghi ở bảng nhiệt dung riêng.
a.
\(Q_{thu}=mc\Delta t=0,25\cdot4200\cdot1,5=1575\left(J\right)\)
b.
Cân bằng nhiệt có: \(Q_{thu}=Q_{toa}=1575\)
\(\Leftrightarrow1575=0,3\cdot c\cdot40=12c\)
\(\Leftrightarrow c=131,25\left(\dfrac{J}{kg}K\right)\)
c.
Tại vì trong quá trình trao đổi thì đã có 1 phần nhiệt toả ra và trao đổi với môi trường nên dẫn đến sự chênh lệch

refer
a) Nhiệt độ cuối cùng của chì cũng là nhiệt độ cuối cùng của nước, nghĩa là bằng 60°C
b) Nhiệt lượng nước thu vào:
Q = m1C1(t – t1) = 4 190.0,25(60 – 58,5)
= 1 571,25J
c) Nhiệt lượng trên do chì tỏa ra, do đó tính nhiệt dung riêng của chì:
C2=Q/m2(t2–t)=1571,25/0,3(100–60)≈130,93J/kg.K

Tóm tắt:
\(m_1=300g=0,3kg\)
\(t_1=100^oC\)
\(m_2=250g=0,25kg\)
\(t_2=58,5^oC\)
\(t=60^oC\)
\(c_2=4200J/kg.K\)
=========
a) \(t=?^oC\)
b) \(Q_2=?J\)
c) \(c_1=?J/kg.K\)
So sánh với nhiệt dung riêng của chì trong bảng:
Giải:
a) Nhiệt độ của chì ngay khi có cân bằng là \(t=60^oC\)
b) Nhiệt lượng nước thu vào:
\(Q_2=m_2.c_2.\left(t+t_2\right)\)
\(\Leftrightarrow Q=0,25.4200.\left(60-58,5\right)=1575J\)
c) Nhiệt dung riêng của chì:
Thep phương tình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=1575\)
\(\Leftrightarrow c_1=\dfrac{1575}{m_1.\left(t_1-t\right)}\)
\(\Leftrightarrow c_1=\dfrac{1575}{0,3.\left(100-60\right)}\)
\(\Leftrightarrow c_1=131,25J/kg.K\)
Nhiệt dung riêng này lớn hơn so với nhiệt dung riêng của chì trong bảng

C3. Để xác định nhiệt dung riêng của một kim loại, người ta bỏ vào nhiệt lượng kế chứa 500 g nước ở nhiệt độ 130C một miếng kim loại có khối lượng 400 g được nung nóng tới 1000C. Nhiệt độ khi có cân bằng nhiệt là 200C. Tính nhiệt dung riêng của kim loại. Bỏ qua nhiệt lượng làm nóng nhiệt lượng kế và không khí. Lấy nhiệt dung riêng của nước là 4 190 J/kg.K
Bài giải:
Nhiệt lượng miếng kim loại tỏa ra:
Q1 = m1 . c1 . (t1 – t) = 0,4 . c . (100 – 20)
Nhiệt lượng nước thu vào:
Q2 = m2 . c2 . (t – t2) = 0,5 . 4190 . (20 – 13)
Nhiệt lượng tỏa ra bằng nhiệt lượng thu vào:
Q1 = Q2
0,4 . c . (100 – 20) = 0,5 . 4190 . (20 – 13)
C = 458 J/kg.K
Kim loại này là thép
Nhiệt lượng miếng kim loại tỏa ra:
Q1 = m1 . c1 . (t1 – t) = 0,4 . c . (100 – 20)
Nhiệt lượng nước thu vào:
Q2 = m2 . c2 . (t – t2) = 0,5 . 4190 . (20 – 13)
Nhiệt lượng tỏa ra bằng nhiệt lượng thu vào:
Q1 = Q2
0,4 . c . (100 – 20) = 0,5 . 4190 . (20 – 13)
C = 458 J/kg.K
Kim loại này là thép.

a) Nhiệt độ của miếng nhôm ngay khi có cân bằng nhiệt là 27oC.
b) Nhiệt lượng do quả cầu tỏa ra
Q1 = m1C1(t1 –t) = 0,2.880.(100 – 27) = 12848J
c) Nhiệt lượng do nước thu vào để tăng nhiệt độ đến 27oC
Q2 = m2C2(t-t2) = m2.4200.(27-20) = \(29400.m_2\)
Áp dụng phương trình cân bằng nhiệt, ta có:
Q1 = Q2 => 12848= \(29400.m_2\)
m2 =\(\frac{12848}{29400}=0,44kg\)
Vậy khối lượng của nước là 0,44kg.

CHÚC BẠN HỌC TỐT !!!!!!!
Giải thích các bước giải:
Chì Nước
m1 = 300 (g) = 0,3 (kg) m2 = 250 (g) = 0,25 (kg)
t1 = 100⁰C t2 = 58,5⁰C c2 = 4200 (J/kg.K)
t = 60⁰C
a)
Vì nước nóng tới 60⁰C nên đó là nhiệt độ sau khi cân bằng => Khi cân bằng nhiệt thì nhiệt độ của chì cũng là 60⁰C.
b)
Nhiệt lượng nước thu vào là:
Q2 = m2.c2.Δt2 = m2.c2.(t - t2)
= 0,25.4200.(60 - 58,5)
= 1575 (J)
c)Theo phương trình cân bằng nhiệt: Q1 = Q2 = 1575 (J)
Nhiệt dung riêng của chì là:
c1 = Q1/m1.Δt1 = Q/m1.(t1 - t)
= 1575/0,3.(100 - 60)
= 131,25 (J/kg.K)
Nhiệt độ cuối của chì cũng là nhiệt độ cuối của nước, nghĩa là \(=60^oC\)
Nhiệt lượng nước thu vào là
\(Q=m_1c_1\Delta t=4,910.0,25.\left(60-58,5\right)\\ =1571,25\left(J\right)\)
Nhiệt lượng trên do chì toả ra, do đó nhiệt dung riêng của chì là
\(C_2=\dfrac{Q}{m_2\Delta t}=\dfrac{1571,25}{0,3\left(100-60\right)}\approx130,93\left(J/kg.K\right)\)

Nhiệt lượng miếng kim loại tỏa ra:
Q1 = m1 . c1 . (t1 – t) = 0,4 . c . (100 – 20)
Nhiệt lượng nước thu vào:
Q2 = m2 . c2 . (t – t2) = 0,5 . 4190 . (20 – 13)
Nhiệt lượng tỏa ra bằng nhiệt lượng thu vào:
Q1 = Q2
0,4 . c . (100 – 20) = 0,5 . 4190 . (20 – 13)
C = 458 J/kg.K
Kim loại này là thép.
Khi xảy ra cân bằng nhau ta có phương trình sau:
Q1 = Q2 <=> 0.5x4190x(20-13)=0.4xCkim loạix(100-20)
<=> 14665=32xCkim loại <=> Ckim loại = 14665:32 = 458,28

Tóm tắt
\(m_1=300g=0,3kg\)
\(t_1=100^0C\)
\(m_2=0,25kg\)
\(t_2=58,5^0C\)
\(t=60^0C\)
____________
a)\(c_1=4200J/kg.K\)
\(Q_2=?J\)
b)\(c_1=?J/kg.K\)
Giải
a)Nhiệt lượng nước thu vào là:
\(Q_2=m_2.c_2\left(t-t_2\right)=0,25.4200\left(60-58,5\right)=1575\left(J\right)\)
b)Nhiệt lượng chì toả ra là:
\(Q_1=m_1.c_1.\left(t_1-t\right)=0,3.c_1.\left(100-60\right)=12c_1\left(J\right)\)
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\)
\(\Leftrightarrow12c_1=1575\)
\(\Rightarrow c_1=131,25J/kg.K\)
c. ơn c nhìu, giúp mk tận 2 câu , giỏi qué>3
, giỏi qué>3