QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
QD
31 tháng 3 2017
a) Góc giữa đường thẳng và mặt phẳng.
Định nghĩa
Cho đường thẳng d cắt mặt phẳng (α) tại điểm O và d không vuông góc với (α). Góc giữa đường thẳng d và mặt phẳng (α) là góc tạo bởi đường thẳng d và hình chiếu vuông góc góc d' của d trên mặt phẳng (α), kí hiệu góc (d,α).
- Nếu d vuông góc góc với (α) ta qui ước góc (d,α) = 90o.
- Nếu d // (α) hay d nằm trong (α) ta quy ước góc (d,α) = 90o.
b) Góc giữa hai mặt phẳng
Định nghĩa : Giả sử hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến c. Từ điểm I bất kì trên c ta dựng trong (α) đường thẳng a vuông góc với c và dựng trong (β) đường thẳng b vuông góc với c. Ta gọi góc giữa hai đường a và b là góc giữa hai mặt phẳng (α) và (β). Như vậy góc giữa hai mặt phẳng (α) và (β) luôn có số đo bé hơn hoặc bằng 90o.
*Nếu hai mặt phẳng song song hoặc trùng với nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0o. Góc giữa hai mặt phẳng (α) và (β) được kí hiệu là (α, β), ta có 0o ≤ (α, β) ≤ 90o.
B
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
Những ví dụ trong thực tiễn minh hoạ hình ảnh hai mặt phẳng vuông góc là: Mặt tường vuông góc với sàn nhà, mặt ngang vuông góc với mặt đứng của bậc thang,…
PT
1
CM
21 tháng 10 2018
a) Định nghĩa: Góc giữa đường thẳng và mặt phẳng.
Cho đường thẳng d cắt mặt phẳng (α) tại điểm O và d không vuông góc với (α). Góc giữa đường thẳng d và mặt phẳng (α) là góc tạo bởi đường thẳng d và hình chiếu vuông góc góc d' của d trên mặt phẳng (α), kí hiệu góc (d,α).
- Nếu d vuông góc góc với (α) ta qui ước góc (d,α) = 90o.
- Nếu d // (α) hay d nằm trong (α) ta quy ước góc (d,α) = 90o.
b) Định nghĩa: Góc giữa hai mặt phẳng
Giả sử hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến c. Từ điểm I bất kì trên c ta dựng trong (α) đường thẳng a vuông góc với c và dựng trong (β) đường thẳng b vuông góc với c. Ta gọi góc giữa hai đường a và b là góc giữa hai mặt phẳng (α) và (β). Như vậy góc giữa hai mặt phẳng (α) và (β) luôn có số đo bé hơn hoặc bằng 90o.
*Nếu hai mặt phẳng song song hoặc trùng với nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0o. Góc giữa hai mặt phẳng (α) và (β) được kí hiệu là (α, β), ta có 0o ≤ (α, β) ≤ 90o.
CM
29 tháng 4 2017
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ
SG
1
QD
1 tháng 4 2017
Xác định thiết diện của hình chóp,hình lăng trụ dựa trên quan hệ vuông góc thường dựa trên các nguyên tắc sau: *Mặt phẳng chứa thiết diện qua một điểm và vuông góc với một đường thẳng thì chứa hai đường thẳng cắt nhau vuông góc với đường thẳng đó. * Mặt phẳng chứa thiết diện qua một đường thẳng và vuông góc với một mặt phẳng thì chứa một đường thẳng vuông góc với mặt phẳng đó.
CM
17 tháng 9 2017
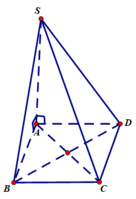
a) SA ⊥ (ABCD), SA ⊂ (SAB) ⇒ (SAB) ⊥ (ABCD)
SA ⊥ (ABCD), SA ⊂ (SAD) ⇒ (SAD) ⊥ (ABCD)
SA ⊥ (ABCD)⇒SA ⊥ BD ⊂(ABCD) và BD ⊥ AC(hai đường chéo hình vuông)
⇒BD ⊥ (SA,AC)⇒BD ⊥ (SAC) mà BD ⊂(ABCD) nên (SAC) ⊥ (ABCD)
b) BD ⊥ (SAC) mà BD ⊂(SBD) nên (SAC) ⊥ (SBD)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có : \(\widehat {xOz} = \widehat {xOy} + \widehat {yOz}\)
21 tháng 8 2023
a: Có thể xác định được bằng cách bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh.
b: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó
Khi đặt thiết bị lên mp nghiêng (Q) thì ta sẽ có:
\(OM\perp\left(Q\right);ON\perp\left(P\right)\)
\(OM\subset\left(P\right),ON\subset\left(Q\right)\)
=>\(\widehat{\left(P\right),\left(Q\right)}=\widehat{\left(OM;ON\right)}=\widehat{MON}=90^0\)
Góc là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc là độ hoặc radian.
Số đo của mỗi góc không vượt quá \({180^ \circ }\)