Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:
Quy tắc 1:
1. Tìm tập xác định.
2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
1. Tìm tập xác định.
2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu xi (i = 1, 2, 3, ...) là các nghiệm của nó.
3. Tính f"(x) và f"(xi)
4. Nếu f"(xi) > 0 thì xi là điểm cực tiểu.
Nếu f"(xi) < 0 thì xi là điểm cực đại.
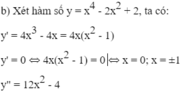
Dựa vào Quy tắc 2, ta có:
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.
y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.

Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.

a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0

Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.

- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
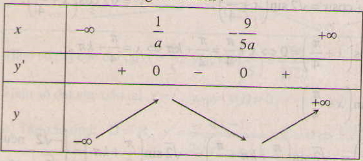
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
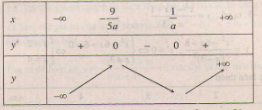
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.

Với \(x\ne2\) ta có \(y=1-\frac{m}{\left(x-2\right)^2}\)
Hàm số có cực đại và cực tiểu \(\Leftrightarrow\) phương trình \(\left(x-2\right)^2-m=0\) (1) có 2 nghiệm phân biệt khác 2 \(\Leftrightarrow m>0\)
Với m>0 phương trình (1) có 2 nghiệm là :
\(x_1=2+\sqrt{m}\Rightarrow y_1=2+m+2\sqrt{m}\)
\(x_2=2-\sqrt{m}\Rightarrow y_2=2+m-2\sqrt{m}\)
Hai điểm cực trị của đồ thị hàm số \(A\left(2-\sqrt{m};2+m-2\sqrt{m}\right);B\left(\left(2+\sqrt{m};2+m+2\sqrt{m}\right)\right)\)
Khoảng cách từ A và B tới d bằng nhau nên ta có phương trình :
\(\left|2-m-\sqrt{m}\right|=\left|2-m+\sqrt{m}\right|\)
\(\Leftrightarrow\begin{cases}m=0\\m=2\end{cases}\)
Đối chiếu điều kiện thì m=2 thỏa mãn bài toán. Vậy yêu cầu bài toán là m=2

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

Ta có : \(y'=3x^2-6mx+3\left(m^2-1\right)\)
Để hàm số có cực trị thì phương trình \(y'=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow x^2-2mx+m^2-1=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1>0\) với mọi m
Cực đại của đồ thị hàm số là A(m-1;2-2m) và cực tiểu của đồ thị hàm số là B (m+1; -2-2m)
Theo giả thiết ta có :
\(OA=\sqrt{2}OB\Leftrightarrow m^2+6m+1\Leftrightarrow\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)
Vậy có 2 giá trị m là \(\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)
Xét hàm số : y = x4 – 2x2 + 2
Có đạo hàm là: y’ = 4x3 – 4x = 0 ⇔ x = 0, x = 1, x = -1
Đạo hàm cấp hai: y’’ = 12x2 – 4
y’’(0) = -4 < 0 ⇒ điểm cực đại xCD =0
y’’(-1) = 8 > 0, y’’(-1) = 8 > 0
⇒ các điểm cực tiểu xCT = -1, xCT = 1