Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

electrong chuyển từ trạng thái dừng n = 3 xuống trạng thái dừng n =2 => nguyên tử hiđrô đã phát ra một năng lượng đúng bằng
\(\Delta E = E_{cao}-E_{thap}= -\frac{13,6}{3^2}-(-\frac{13,6}{2^2})= 13,6.(\frac{1}{4}-\frac{1}{9})= 1,89 eV= 1,89.1,6.10^{-19}V.\)
Mà \(\Delta E = \frac{hc}{\lambda}=> \lambda = \frac{hc}{\Delta E}= \frac{6,625.10^{-34}.3.10^8}{1,89.1,6.10^{-19}}= 6,57.10^{-7}m = 0,657 \mu m.\)

+ Áp dụng tiên đề Bo về bức xạ và hấp thụ năng lượng, ta có :
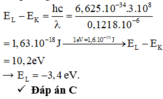

+ Áp dụng tiên đề Bo về bức xạ và hấp thụ năng lượng, ta có :


Đáp án C
Áp dụng tiên đề Bo về hấp thụ và bức xạ năng lượng thì ta có :
![]()
![]()

Bước sóng dài nhất trong dãy Banme là \(\lambda_1\Rightarrow\frac{hc}{\lambda_1}=E_3-E_2\)(1)
Bước sóng dài nhất trong dãy Laiman là \(\lambda_2\Rightarrow\frac{hc}{\lambda_2}=E_2-E_1\)(2)
Bước sóng dài thứ 2 trong dãy Laiman là \(\lambda_3\Rightarrow\frac{hc}{\lambda_3}=E_3-E_1\)(3)
Lấy (1) + (2) vế với vế ta đc: \(\frac{hc}{\lambda_1}+\frac{hc}{\lambda_2}=E_3-E_1=\frac{hc}{\lambda_3}\)
\(\Rightarrow\frac{1}{\lambda_3}=\frac{1}{\lambda_1}+\frac{1}{\lambda_2}\)
\(\Rightarrow\lambda_3=0,1029\mu m\)

Đáp án D
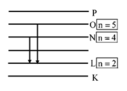 *Khi nguyên tử phát chuyển từ quỹ đạo có mức năng lượng cao về mức năng lượng thấp thì sẽ phát ra một phôtôn có bước sóng
*Khi nguyên tử phát chuyển từ quỹ đạo có mức năng lượng cao về mức năng lượng thấp thì sẽ phát ra một phôtôn có bước sóng
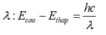
![]()
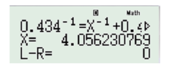 *Nhận thấy hiệu năng lượng tỉ lệ nghịchvới bước sóng tương ứng.
*Nhận thấy hiệu năng lượng tỉ lệ nghịchvới bước sóng tương ứng.
![]()
![]()
Kinh nghiệm: Khi bài toán cho 2 bước sóng yêu cầu tìm bước sóng còn lại ta làm nhanh như sau:
Bước 1: Biểu diễn các bước sóng liên quan trên sơ sơ đồ mức năng lượng . Tính độ dài xoay quanh các quỹ đạo liên quan đến bài toán (Ví dụ ở bài trên thì OL=ON+LN)
Bước 2: Thay các độ dài đó bằng nghịch đảo các bước sóng (nếu đề cho các bước sóng). Thay tần số (nếu đề cho tần số) tương ứng.
Bước 3: Dùng chức năng SHIFT –SOLVE giải nhanh ẩn số còn lại.

Chọn đáp án D.
*Khi nguyên tử phát chuyển từ quỹ đạo có mức năng lượng cao về mức năng lượng thấp thì sẽ phát ra một phôtôn có bước sóng λ thỏa mãn
E c a o − E t h a p = h c λ
E 5 − E 3 = E 5 − E 4 − E 4 − E 3
*Nhận thấy hiệu năng lượng tỉ lệ nghịchvới bước sóng tương ứng
λ 53 − 1 = λ 54 − 1 + λ 43 − 1 ⇔ 0 , 434 − 1 = λ 54 − 1 + 0 , 486 − 1
λ 54 = 4 , 056 μ m

bước sóng ngắn nhất của hidro là bước sóng từ lớp \(\infty\) về lớp K
sử dụng công thức
R\(\infty\) x (\(\frac{1}{1^2}\) - \(\frac{1}{\infty}\)) = \(\frac{1}{10973731,57}\)
=> \(\lambda=\frac{1}{10973731,57}\) = \(^{9,11.10^{-8}}\)m \(\approx\) 0,0913 \(\mu m\)
=> đáp án B
ở đây tớ chỉ giải mẹo theo công thức đó. muốn biết thêm cách giải mẹo này thì cmt nhé!!![]()
Năng lượng ion hóa là năng lượng tối thiểu để có thể tách một electron ra khỏi nguyên tử để trở thành electron tự do.
Khi nguyên tử hiđrô hấp thụ năng lượng bằng 13,6 eV thì năng lượng của nguyên tử lúc này là 0 eV ứng với việc nó có thể phát ra một phôtôn có bước sóng ngắn nhất thỏa mãn
\(\frac{hc}{\lambda}= E_0-E_1 = 0-(-13,6)= 13,6 eV.\)
=> \(\lambda _ {min}= \frac{6,625.10^{-34}.3.10^8}{13,6.1,6.10^{-19}}= 9,13.10^{-8}m= 0,0913 \mu m..\)
Năng lượng ion hóa là năng lượng tối thiểu để có thể tách một electron ra khỏi nguyên tử để trở thành electron tự do.
Khi nguyên tử hiđrô hấp thụ năng lượng bằng 13,6 eV thì năng lượng của nguyên tử lúc này là 0 eV ứng với việc nó có thể phát ra một phôtôn có bước sóng ngắn nhất thỏa mãn
hc/λ=E0−E1=0−(−13,6)=13,6eV.
=> λmin=6,625.10−34.3.10813,6.1,6.10−19=9,13.10−8m=0,0913μm..