Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có:
\(L=50\Leftrightarrow10log\left(\dfrac{I}{I_0}\right)=50\\ \Leftrightarrow\dfrac{I}{I_0}=10^5\\ \Leftrightarrow I=I_0\cdot10^5=10^{-12}\cdot10^5=10^{-7}\left(W/m^2\right)\)
Vậy cường độ âm của giọng nói giáo viên là \(I=10^{-7}\left(W/m^2\right)\)
b, Ta có:
\(75\le L\le90\Leftrightarrow75\le10log\left(\dfrac{I}{I_0}\right)\le90\Leftrightarrow10^{7,5}\le\dfrac{I}{10^{-12}}\le10^9\\ \Leftrightarrow10^{-4,5}\le I\le10^{-3}\\ \Leftrightarrow3,16\cdot10^{-5}\le I\le10^{-3}\)
Vậy cường độ âm trong nhà xưởng này thay đổi trong khoảng \(3,16\cdot10^{-5}\left(W/m^2\right)\) đến \(10^{-3}\left(W/m^2\right)\)

a: Mức cường độ âm là:
\(L=10\cdot log\left(\dfrac{l}{l0}\right)=10\cdot log\left(\dfrac{10^{-12}}{10^{-12}}\right)=20\left(dB\right)\)
b;
Để âm thanh không gây hại cho tai thì âm thanh cần phải có cường độ âm không vượt quá:
\(L=100000\cdot10^{-10}=10^{-5}\left(\dfrac{W}{m^2}\right)\)
Cường độ âm cần phải không vượt quá là:
\(10\cdot log\left(\dfrac{10^{-5}}{10^{-12}}\right)=70\left(dB\right)\)
a) Mức cường độ âm của tiếng thì thầm là:
\(L=10log\dfrac{10^{-10}}{10^{-12}}=20\left(dB\right)\)
b) Để âm thanh không gây hại cho tai khi nghe thời gian dài thì cường độ âm là:
\(I=100000.10^{-10}=10^{-5}\left(W/m^2\right)\)
Mức cường độ âm giới hạn đó là:
\(L=10log\dfrac{10^{-5}}{10^{-12}}=70\left(dB\right)\)

Mức cường độ âm được tính theo công thức: \(L=log\dfrac{I}{I_0}\left(B\right)\)
Giới hạn tai người nghe được là:
\(\left\{{}\begin{matrix}L=log\dfrac{10^{-12}}{10^{-12}}=0\left(B\right)\\L=log\dfrac{10}{10^{-12}}=13\left(B\right)\end{matrix}\right.\)
Vậy tai người nghe được mức cường độ âm từ 0 - 13B

a, Vì cường độ ánh sáng giảm dần theo độ sâu nên hàm số \(I=I_0\cdot a^d\) nghịch biến.
Vậy 0 < a < 1.
b, Ta có: \(I=I_0\cdot a^d\Rightarrow0,95I_0=I_0\cdot a^1\Leftrightarrow a=0,95\)
c, Ta có: \(I=I_0\cdot a^d=I_0\cdot0,95^{20}\approx0,36I_0\)
Vậy tại độ sâu 20m, cường độ ánh sáng bằng 36% so với \(I_0\)

Gọi (un) là dãy số thể hiện quãng đường di chuyển của quả bóng sau mỗi lần chạm đất.
Ta có: \({u_1} = 55,8;{u_2} = \frac{1}{{10}}.{u_1};{u_3} = {\left( {\frac{1}{{10}}} \right)^2}.{u_1};...;{u_n} = {\left( {\frac{1}{{10}}} \right)^{n - 1}}.{u_1}.\)
Khi đó dãy (un) lập thành một cấp số nhân lùi vô hạn có số hạng đầu u1 = 55,8 và công bội \(q = \frac{1}{{10}}\) thỏa mãn \(\left| q \right| < 1.\)
\( \Rightarrow {S_n} = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{55,8}}{{1 - \frac{1}{{10}}}} = 62\left( m \right)\)
Vậy tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất n lần là 62 m.

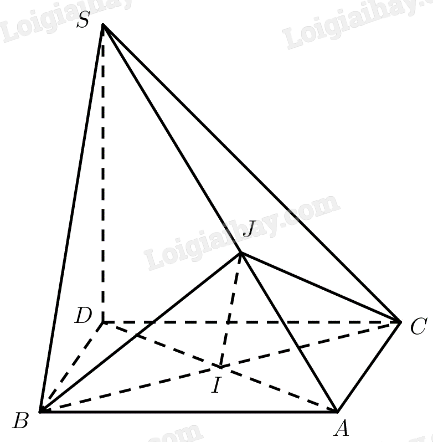
a) \(ABC{\rm{D}}\) là hình thoi \( \Rightarrow A{\rm{D}} \bot BC\)
\(S{\rm{D}} \bot \left( {ABC} \right) \Rightarrow S{\rm{D}} \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SA{\rm{D}}} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
b) Kẻ \(IJ \bot SA\left( {J \in SA} \right)\).
\(\Delta ABC\) đều \( \Rightarrow AI = \frac{{a\sqrt 3 }}{2} \Rightarrow A{\rm{D}} = 2AI = a\sqrt 3 \)
\(\Delta SAD\) vuông tại \(D\) \( \Rightarrow S{\rm{A}} = \sqrt {S{D^2} + A{{\rm{D}}^2}} = \frac{{3a\sqrt 2 }}{2}\)
Tam giác \(BCJ\) có \(IJ\) là trung tuyến và \(IJ = \frac{1}{2}BC\)
Vậy tam giác \(BCJ\) vuông tại \(J \Rightarrow BJ \bot JC\)
\(\begin{array}{l}\left. \begin{array}{l}BC \bot \left( {SA{\rm{D}}} \right) \Rightarrow BC \bot SA\\IJ \bot SA\end{array} \right\} \Rightarrow SA \bot \left( {BCJ} \right)\\\left. \begin{array}{l} \Rightarrow SA \bot BJ\\BJ \bot JC\end{array} \right\} \Rightarrow BJ \bot \left( {SAC} \right)\end{array}\)
Mà \(BJ \subset \left( {SAB} \right)\)
Vậy \(\left( {SAB} \right) \bot \left( {SAC} \right)\).

a:
i:
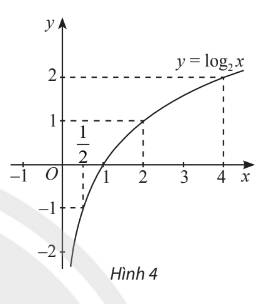
| x | 1/2 | 1 | 2 | 4 |
| y | -1 | 0 | 1 | 2 |
ii:
Hàm số liên tục và đồng biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_2x=+\infty;\lim\limits_{x\rightarrow0^+}log_2x=-\infty\)
Tập giá trị: R
b:
| x | 1/2 | 1 | 2 | 4 |
| y | 1 | 0 | -1 | -2 |
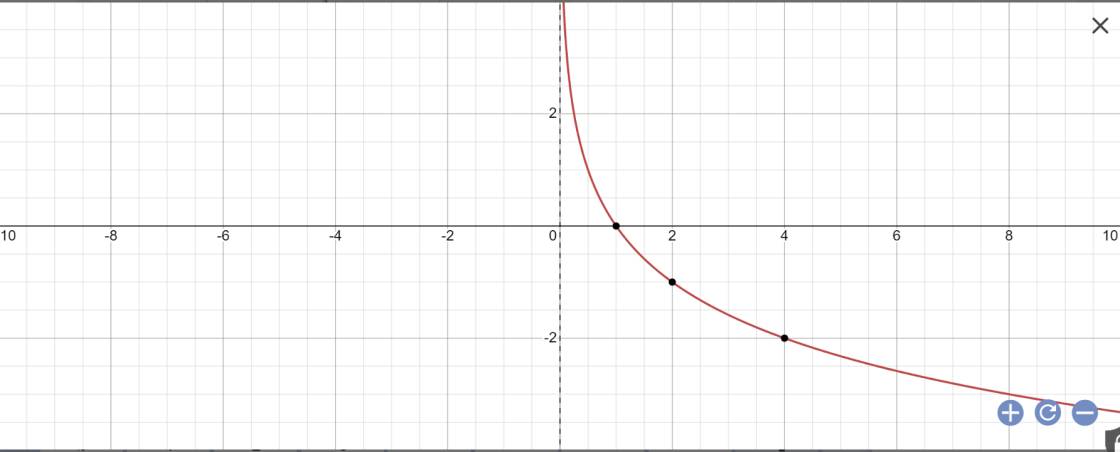
Hàm số liên tục và nghịch biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_{\dfrac{1}{2}}x=-\infty;\lim\limits_{x\rightarrow0^+}log_{\dfrac{1}{2}}x=+\infty\)
Tập giá trị: R



a: Mức cường độ âm là:
\(L=10\cdot log\left(\dfrac{10^{-7}}{10^{-12}}\right)=10\cdot log\left(10^5\right)=50\left(dB\right)\)
b: Mức cường độ âm khi giao thông đông đúc là:
\(L=10\cdot log\left(\dfrac{10^{-3}}{10^{-12}}\right)=90\left(dB\right)\)