K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
2
19 tháng 8 2018
\(A=9x^2+18x-20\)
\(\Leftrightarrow A=\left(3x\right)^2+2.3x.3+9-29\)
\(\Leftrightarrow A=\left(3x+3\right)^2-29\le-29\forall x\)
Dấu " = " xảy ra
\(\Leftrightarrow\left(3x+3\right)^2=0\Leftrightarrow3x+3=0\Leftrightarrow3x=-3\Leftrightarrow x=-1\)
Vậy Min A là : \(-29\Leftrightarrow x=-1\)
\(B=m^2+10m+1\)
\(\Leftrightarrow B=m^2+2.m.5+25-24\)
\(\Leftrightarrow B=\left(m+5\right)^2-24\le-24\forall m\)
Dấu \("="\) xảy ra
\(\Leftrightarrow\left(m+5\right)^2=0\Leftrightarrow m+5=0\Leftrightarrow m=-5\)
Vậy Min B là : -24 \(\Leftrightarrow m=-5\)
\(C=25x^2-20x+30\)
\(\Leftrightarrow C=\left(5x\right)^2-2.5x.2+4+26\)
\(\Leftrightarrow C=\left(5x-2\right)^2+26\le26\forall x\)
Dấu " = " xảy ra
\(\Leftrightarrow\left(5x-2\right)^2=0\Leftrightarrow5x-2=0\Leftrightarrow5x=2\Leftrightarrow x=\dfrac{2}{5}\)
Vậy Min C là : 26 \(\Leftrightarrow x=\dfrac{2}{5}\)
30 tháng 11 2017
Ta có:\(p=\left(m^2-4mn+4n^2\right)+\left(10m-20n\right)+25+\left(n^2-2n+1\right)+6\)
\(\Rightarrow p=\left(m-2n\right)^2+2.5\left(m-2n\right)+5^2+\left(n-1\right)^2+6\)
\(\Rightarrow p=\left(m-2n+5\right)^2+\left(n-1\right)^2+6\ge6\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}m-2n+5=0\\n-1=0\end{cases}}\Rightarrow\hept{\begin{cases}m=-3\\n=1\end{cases}}\)
Vậy GTNN của p=6 khi m=-3 ; n=1
4 tháng 4 2016
A = (m2 -4mp + 4p2 ) + (p2 -2p + 1) + 27 + 10m - 20p = (m-2p)2 + (p-1)2 27 + 10(m-2p)
Đặt X = m-2p.
Ta có A=x2 + 10X + 27 + (p-1)2 = (X2 + 10X + 25) + (p-1)2 + 2 = (X+5)2 + (p-1)2 + 2
Ta thấy: (X + 5)^2> 0 với m, p; (p-1)^2> 0 p Do đó: A đạt giá trị nhỏ nhất khi: Vậy Min A=2 khi m=-3; p=1
Có bài số ko hỏi tớ-_-
15 tháng 10 2022
a: \(A=m^6-6m^5+10m^4+m^3+98m-26\)
\(=m^6-m^4+m^3-6m^5+6m^3-6m^2+11m^4-11m^2+11m-6m^3+6m-6+17m^2+81m-20\)
\(=m^3-6m^2+11m-6+\dfrac{17m^2+81m-20}{m^3-m+1}\)
\(C=m^3-6m^2+11m-6=\left(m-1\right)\left(m-3\right)\left(m-2\right)\) luôn chia hết cho 6
b: Để đa thức dư bằng 0 thì 17m^2+81m-20=0
=>m=-5 hoặc m=4/17
25 tháng 12 2017
Mk chỉ giúp phần tách thôi nha
3. A=x2-2xy+2y2+2x-10y+2033
=(x2-2xy+y2)+(y2-10y+25)+2x+2008
=(x2-2xy+y2)+(y2-10y+25)+(x2+2x+1)-x2+2007
=(x-y)2+(y-25)2+(x+1)2-x2+2007
Vì....
không bt là có đúng k đâu
CT
Tìm giá trị nhỏ nhất của biểu thức sau:
D = m2 - 4mp + 5p2 + 10m - 22p + 20
Mình chưa bt làm câu này ạ
1
YN
13 tháng 12 2021
Answer:
\(D=m^2-4mp+5p^2+10m-22p+20\)
\(=m^2-4mp+4p^2+p^2+10m-20p-2p+1+19\)
\(=\left(m^2-4mp+4p^2\right)+\left(10m-20p\right)+\left(p^2-2p+1\right)+19\)
\(=\left(m-2p\right)^2+10\left(m-2p\right)+\left(p-1\right)^2+25-6\)
\(=[\left(m-2p\right)^2+10\left(m-2p\right)+25]+\left(p-1\right)^2-6\)
\(=\left(m-2p+5\right)^2+\left(p-1\right)^2-6\)
\(\forall m;p\) có \(\left(m-2p+5\right)^2+\left(p-1\right)^2-6\ge-6\) hay \(D\ge-6\)
Dấu "=" xảy ra khi:
\(\hept{\begin{cases}\left(m-2p+5\right)^2=0\\\left(p-1\right)^2=0\end{cases}}\Rightarrow\hept{\begin{cases}m-2p+5=0\\p-1=0\end{cases}}\Rightarrow\hept{\begin{cases}m-2p+5=0\\p=1\end{cases}}\Rightarrow\hept{\begin{cases}m-2.1+5=0\\p=1\end{cases}}\Rightarrow\hept{\begin{cases}m=-3\\p=1\end{cases}}\)
Vậy giá trị nhỏ nhất của biểu thức \(D=-6\) khi \(\hept{\begin{cases}m=-3\\p=1\end{cases}}\)
PN
14 tháng 3 2016
Bài khó xơi trước để mát dạ đã rồi tính
\(3.\) Điều kiện để phương trình trên có nghĩa \(a\ne0;\) \(b\ne0\) và \(c\ne0\) (theo giả thiết)
Trừ \(1\) vào mỗi phân thức ở \(VT\) và trừ \(3\) cho \(VP\), ta được:
\(\frac{x-a-b-c}{a}+\frac{x-a-b-c}{b}+\frac{x-a-b-c}{c}=0\)
\(\Leftrightarrow\) \(\left(x-a-b-c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=0\) \(\left(\text{*}\right)\)
\(\text{*)}\) Nếu \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ne0\) thì \(\left(\text{*}\right)\) \(\Rightarrow\) \(x-a-b-c=0\), tức \(x=a+b+c\)
\(\text{*)}\) Nếu \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\) thì từ \(\left(\text{*}\right)\), ta suy ra phương trình trên có nghiệm luôn đúng với mọi \(x\)
Vậy, phương trình có nghiệm là \(x=a+b+c\) với trường hợp \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ne0\)
và \(S=R\) nếu \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
PN
14 tháng 3 2016
\(1.\) Gọi \(x\) \(\left(m\right)\) là chiều rộng ban đầu của miếng đất hình chữ nhật.
nên chiều rộng của miếng đất sau khi tăng lên \(10\) \(\left(m\right)\) là \(x+10\) \(\left(m\right)\)
Vì chu vi của miếng đất là \(160\) \(\left(m\right)\) nên nửa chu vi của miếng đất đó sẽ bằng \(80\) \(\left(m\right)\)
Khi đó, chiều dài ban đầu: \(80-x\) \(\left(m\right)\) nên khi giảm đi \(10\) \(\left(m\right)\) thì chiều dài mới là \(70-x\) \(\left(m\right)\)
Điều kiện: \(x<70\)
Ta có phương trình:
\(\left(70-x\right)\left(x+10\right)-x\left(80-x\right)=200\) \(\Leftrightarrow\) \(x=25\) (thỏa mãn điều kiện)
Do đó, chiều dài ban đầu \(80-25=55\) \(\left(m\right)\)
Vậy, ......
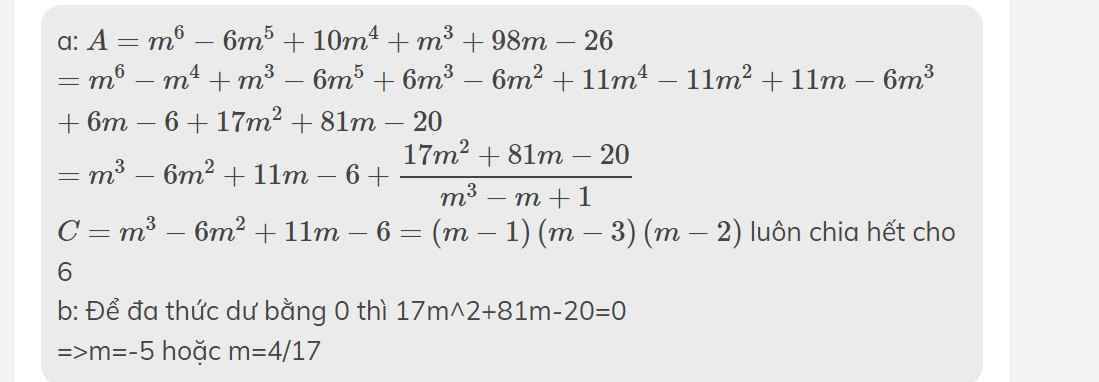
Lời giải:
$m^2+10m+2250=0$
$\Leftrightarrow m^2+2.5m+25+2225=0$
$\Leftrightarrow (m+5)^2=-2225< 0$ (vô lý)
Do đó pt vô nghiệm.