Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Chọn hệ trục Ox như hình vẽ
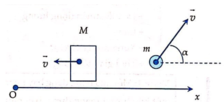
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox
![]()
Vì trước khi bắn hệ đứng yên
Chiếu phương trình (*) lên Ox ta được: 0 = -p’1 + p’2.cos60o
Thay số ta được:
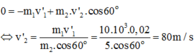

Chọn C.
Chọn hệ trục Ox như hình vẽ
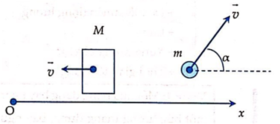
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox


Chọn chiều dương là chiều nòng súng hướng phía trc.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1\cdot v_1\cdot cos45^o+m_2\cdot v_2=0\)
\(\Rightarrow4000\cdot v_1\cdot cos45^o+10\cdot500=0\)
\(\Rightarrow v_1\approx1,77\)m/s

Chọn chiều dương là chiều chuyển động của viên đạn
ÁP dụng định luật bảo toàn động lượng ta có:
\(m_2v_2cos60-m_1v_1=0=>v_2=\dfrac{m_1v_1}{m_2cos60}=\dfrac{7500.1}{20.cos60}=750(m/s)\)
=> Chọn B

Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v → ⇒ V = − m M = − 3 m / s
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.
Chọn đáp án D

Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v →
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.

Giả sử thời gian đạn rời khỏi nòng súng là (rất nhỏ).
Giả sử nội lực của hệ đạn + nòng súng là N.
N làm biến thiên động lượng của đạn (đề đã bỏ qua tác động của trọng trường với đạn).
Hợp lực của N và F ma sát và P làm biến thiên động lượng của nòng.
Chiếu lên phương ngang.
Thay N từ pt trên vào ta tìm được V.

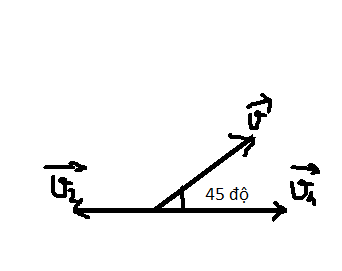
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
\(\Rightarrow p_2\cdot cos\alpha-p_1=0\)
\(\Rightarrow m_2\cdot v_2\cdot cos\alpha-m_1\cdot v_1=0\)
\(\Rightarrow v_2=\dfrac{m_1\cdot v_1}{m_2\cdot cos\alpha}=\dfrac{8000\cdot500}{2\cdot cos60^o}=4\cdot10^6\)m/s