Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì thời gian thực tế đi chậm hơn thời gian dự định là 18 phút nên ta có phương trình:
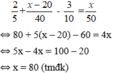
Vậy chiều dài quãng đường AB là 80km.

Gọi chiều dài quãng đường AB là \(x\left( {km} \right)\). Điều kiện \(x > 0\).
Vì ban đầu xe dự định đi với vận tốc 50 \(km/h\) trên suốt quãng đường nên thời gian dự định đi hết quãng đường AB là \(\frac{x}{{50}}\) (giờ).
\(\frac{2}{3}\) quãng đường đầu tiên là \(\frac{2}{3}x\) đi với vận tốc 50 \(km/h\) nên thời gian đi hết \(\frac{2}{3}\) quãng đường đầu tiên là \(\frac{2}{3}x:50 = \frac{2}{{150}}x\) (giờ).
\(\frac{1}{3}\) quãng đường đầu tiên là \(\frac{1}{3}x\) đi với vận tốc 40 \(km/h\) nên thời gian đi hết \(\frac{1}{3}\) quãng đường sau là \(\frac{1}{3}x:40 = \frac{1}{{120}}x\) (giờ).
Tổng thời gian đi thực tế là \(\frac{2}{{150}}x + \frac{1}{{120}}x\) (giờ)
Đổi 30 phút = \(\frac{1}{2}\) giờ
Vì ô tô đến B chậm hơn dự định \(\frac{1}{2}\) giờ nên ta có phương trình:
\(\frac{2}{{150}}x + \frac{1}{{120}}x - \frac{x}{{50}} = \frac{1}{2}\)
\(\frac{{2.4}}{{150.4}}x + \frac{{1.5}}{{120.5}}x - \frac{{x.12}}{{50.12}} = \frac{{1.300}}{{2.300}}\)
\(\frac{{8x}}{{150.4}} + \frac{{5x}}{{120.5}} - \frac{{12x}}{{50.12}} = \frac{{300}}{{600}}\)
\(8x + 5x - 12x = 300\)
\(x = 300\) (thỏa mãn điều kiện)
Vậy độ dài quãng đường AB là 300 \(km\).

Gọi quãng đường AB= s
thời gian xe con đi hết quãng đường AB t1= s/v1 +2/3 = s/60+2/3
thời gian xe tải đi hết quãng đường AB t2= s/(2v2) +s/2(v2+10) = s/80 +s/100
t2= t1+1/2 ---> s/80+ s/100 = s/60 +2/3 +1/2.
Giải phương trình trên ta được s= 200 km
Một tàu thủy chạy trên khúc sông dài 80km, cả đi cả về mất 8 giờ 20 phút. Tính vận tốc của tàu khi nước yên lặng, biết rằng vận tốc của dòng nước là 4 km/h.

15p=0,25h
gọi điểm 2 xe gặp nhau lần 1 là c
điểm hai xe gặp nhau lần 2 là d
độ dài từ c đến d là x
khi xe máy gặp ô tô lần 1 thì xe mấy đi được: 0,25.40=10
quãng đường ô tto đã đi khi gặp xe máy lần 1 đến khi gặp xe máy lần 2 là:10+10+x=20+x
thời gian ô tô đã đi khi gặp nhau lần 1 đến lần 2 là:\(\frac{20+x}{50}\vec{+\frac{1}{4}}\)
thời gian xe máy đi từ lần gặp 1 đến lần gặp 2 là : x/40
=>ta có pt
\(\frac{x}{40}\vec{=\frac{20+x}{50}\vec{+\frac{1}{4}}}\)
giải pt ta đc x=85(km)

Bài giải
Gọi quãng đường AB là x (km) (x \(\inℕ^∗\))
=> Thời gian để ô tô đi từ A đến B với vận tốc 40 km/h và không gặp chướng ngại vật nào là: x : 40
Theo đề bài: 40.1 + 48.(x : 40 - 1,5) = x
=> 40 + 48.x : 40 - 48.1,5 = x
=> 40 + 1,2.x - 72 = x
=> 72 - 40 = 1,2.x - x
=> 32 = 0,2.x
=> x = 32 : 0,2
=> x = 160 (km)
Vậy quãng đường AB dài 160 km

-Gọi quãng đường AB là x (km) (x>0)
-Đổi 15 phút=\(\dfrac{1}{4}\)h ; 10 phút=\(\dfrac{1}{6}\)h
-Quãng đường người đó đi được trong 15 phút đầu: \(40.\dfrac{1}{4}=10\left(km\right)\)
Quãng đường còn lại (km) Vận tốc (km/h) Thời gian (h)
Dự định x-10 40 \(\dfrac{x-10}{40}\)
Thực tế x-10 36 \(\dfrac{x-10}{36}\)
-Quãng đường còn lại xe đi được là: x-10 (km)
-Thời gian xe đi hết quãng đường còn lại dự định: \(\dfrac{x-10}{40}\)(h)
-Thời gian xe đi hết quãng đường còn lại dự thực tế: \(\dfrac{x-10}{36}\)(h)
-Vì xe tải đến B chậm hơn 10 phút so với dự định nên ta có phương trình sau:
\(\dfrac{x-10}{36}-\dfrac{x-10}{40}=\dfrac{1}{6}\)
\(\Leftrightarrow\left(x-10\right)\left(\dfrac{1}{36}-\dfrac{1}{40}\right)=\dfrac{1}{6}\)
\(\Leftrightarrow\left(x-10\right).\dfrac{1}{360}=\dfrac{1}{6}\)
\(\Leftrightarrow x-10=60\)
\(\Leftrightarrow x=70\left(km\right)\left(nhận\right)\)
-Vậy quãng đường AB dài 70 km.