Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc tọa độ trùng với điểm xe bắt đầu hãm phanh
chiều dương của trục trùng với chiều chuyển động
a,Phương trình chuyển động của xe là:
\(40=v_0\cdot5+\dfrac{1}{2}a\cdot5^2\)(1)
Gia tốc của vật :\(a=\dfrac{0-v_0}{4}\Rightarrow v_0+4a=0\)(2)
Từ(1) và (2)
\(\Rightarrow v_0=\dfrac{64}{3}\left(\dfrac{m}{s}\right);a=-\dfrac{16}{3}\left(\dfrac{m}{s^2}\right)\)
vậy...
b, <chỗ quãng đường xe đi thì mình ko hiểu nên mình bỏ qua nha>
Phương trình vận tốc của xe:
\(v=\dfrac{64}{3}-\dfrac{16}{3}t\left(\dfrac{m}{s}\right)\)
c, Phương trình chuyển động của xe trong 10 m cuối là
\(40=30+\dfrac{64}{3}\cdot t-\dfrac{1}{2}\cdot\dfrac{16}{3}t^2\Rightarrow\left[{}\begin{matrix}t=7,5\left(h\right)\left(L\right)\\t=0,5\left(h\right)\left(N\right)\end{matrix}\right.\)
Vì xe dừng lại sau 4 giây kể từ lúc hãm phanh nên loại đáp án t=7,5(h)
Vậy ...
a chết câu b mình ghi nhầm mình đã đăng lại bạn vô ktra giúp hộ mình đáp án với nhé hic

Quãng đường đi được trong 1s cuối
\(\dfrac{1}{2}\cdot a\cdot5^2-\dfrac{1}{2}\cdot a\cdot\left(5-1\right)^2=1,5\Rightarrow a=\dfrac{1}{3}\left(\dfrac{m}{s^2}\right)\)
Vậy gia tốc của vật là 1/3 (m/s^2)
Quãng đường đi dc từ khi hãm phanh đến khi dừng lại
\(s=\dfrac{1}{2}\cdot\dfrac{1}{3}\cdot5^2=\dfrac{25}{6}\left(m\right)\)
<chỗ nào sai chỉ mình hoặc ko hiểu thì bình luận câu trả lời nha>
\(v^2-v^2_0=2as\)
\(\Rightarrow5^2-v^2_0=2a.10\)
\(\Rightarrow25-v^2_0=20a\left(1\right)\)
Lại có: \(10^2-v^2_0=2a.47,5\)
\(\Rightarrow100-^2_0=95a\left(2\right)\)
Từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}25-v^2_0=20a\\100-v^2_0=95a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1m\text{/ }s^2\\v_0=\sqrt{5m\text{/ }s}\end{matrix}\right.\)

Đổi 36km/h=10m/s
Ta có:
Gia tốc chuyển động của xe máy là:
v 2 − v 0 2 = 2 a s → a = v 2 − v 0 2 2 s = − 10 2 2.25 = − 2 m / s 2
Mặt khác, ta xác định vận tốc của xe lúc bắt đầu đi quãng đường 4m4m cuối cùng trước khi dừng lại:
v 2 − v ' 2 = 2 a s → − v ' 2 = 2 a s → v ' = 2 a s = 2.4.2 = 4 m / s
Ta có: v=v′+at
Thời gian đi hết 4m cuối cùng là:
t = v − v ' a = 0 − 4 − 2 = 2 s
Đáp án: D

Để tính giá trị gia tốc, ta sử dụng công thức: v^2 = u^2 + 2as Trong đó: v là vận tốc cuối cùng (0 m/s, vì xe dừng lại) u là vận tốc ban đầu (10 m/s) a là gia tốc s là độ dài vết phanh (5 m) 0^2 = 10^2 + 2a(5) 0 = 100 + 10a 10a = -100 a = -10 m/s^2 Vậy, giá trị gia tốc là -10 m/s^2. Để tính thời gian từ lúc hãm phanh đến lúc dừng lại, ta sử dụng công thức: v = u + at Trong đó: v là vận tốc cuối cùng (0 m/s) u là vận tốc ban đầu (10 m/s) a là gia tốc (-10 m/s^2) t là thời gian 0 = 10 + (-10)t -10t = -10 t = 1 s Vậy, thời gian từ lúc hãm phanh đến lúc dừng lại là 1 giây. Để tính thời gian xe đi trong 2m cuối trước khi dừng, ta sử dụng công thức: s = ut + (1/2)at^2 Trong đó: s là độ dài (2 m) u là vận tốc ban đầu (10 m/s) a là gia tốc (-10 m/s^2) t là thời gian 2 = 10t + (1/2)(-10)t^2 2 = 10t - 5t^2 5t^2 - 10t + 2 = 0 Giải phương trình trên ta có hai giá trị t, nhưng chỉ có giá trị dương mới có ý nghĩa trong bài toán: t ≈ 0.553 s Vậy, thời gian xe đi trong 2m cuối trước khi dừng lại là khoảng 0.553 giây.

a) 72 km/h = 20 m/s
\(v_2^2\) - \(v_1^2\) = 2as
↔ 0 - \(20^2\) = 2.a.500
↔ -400 = 1000.a ↔ a = 0,4
➙ Gia tốc của xe là 0,4 \(m^2\)/s
b)
\(v_2\) - \(v_1\) = at
↔ 0 - 20 = -0,4t
↔ -20 = -0,4t ↔ t = \(\dfrac{-20}{-0,4}\) = 50 (giây)
Nhấn vào \(\Sigma\) là gõ được cái \(\Leftrightarrow\) chứ đâu cần cái ↔️ nhỉ:)?
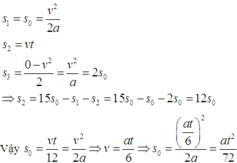
<okie cậu luôn>
<Vì là từ giây cuối đến khi dừng lại nên mình mới có t=1 nha>
b,Quãng đường xe đi dc trong giây cuối trước khi dừng lại
\(s=\dfrac{64}{3}\cdot1-\dfrac{1}{2}\cdot\dfrac{16}{3}\cdot1^2=\dfrac{56}{3}\left(m\right)\)
mình làm cái này cho bạn rùi nha
https://hoc24.vn/cau-hoi/mot-xe-dang-chuyen-dong-thi-tai-xe-dap-thang-xe-con-di-duoc-40m-trong-thoi-gian-4s-thi-dung-laia-tim-vat-toc-ban-dau-va-gia-toc-cua-xeb-tim-quang-d.1810464749011