Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-khoảng thời gian 2 lần liên tiếp qua vị trí cân bằng là o,5s có nghĩa là trong 0,5 s đó vật đi dc 2A ( vì ta biết là vật dao động từ VTCB đến điểm biên rùi trở lại VTCB .đoạn đó =2A nhá)
- Ta bjk 1 chu kì là 4A vậy 2A là 1/2 chu kì, mà tg đi 2A = 0,5s vậy 4A =1s, suy ra T=1s,..
- Quãng đường vật đi dc trong 2s là 32cm, vì T=1s nên 2s là 2T mà 2s đi dc 32 cm, nên 8A=32 ( vì T=4A chắc ai cũng bjk  ) => A =4cm ..
) => A =4cm ..
- T=1 => ω =2 tt ( tt nghĩa là số pi nhá).
- bi giờ đi tìm pha ban đầu (ψ )
ta có pt : x = Acos(ωt + ψ)
-tại t=1,5 thì x= 2√3 thế vô ta dc:
2√3=4cos(2 tt * 1,5 + ψ)
=> ψ = - tt/6
Vậy PT là : x= 4cos(2 tt * t - tt/6)..|-)

\(\omega\)=2\(\pi\)f=2\(\pi\).5=10\(\pi\)
A=4 vật qua VTCB theo chiều dương=> v>0 =>\(\varphi\)<0
Nhìn đáp án ta chọn C
Nếu có j thắc mắc thì hỏi mình nha bạn!!

Đáp án B
Giả sử x = Acos ( ωt + φ )
Thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là nửa chu kỳ nên
![]()
Quãng đường đi được trong 2s (2 chu kì) là: S=2.4A=32 =>A=4cm
Tại thời điểm t=1,5s vật qua vị trí có li độ 2 3 cm theo chiều dương
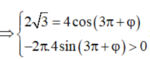
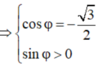
Suy ra, có thể lấy φ = - 7 π 6

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ \(\omega = 2\pi f = 2\pi .10 = 20\pi \ (rad/s) \)
+ A = 4cm.
+ t = 0, vật qua x0 = A \(\Rightarrow\left\{ \begin{array}{} x_0 = 4\ cm\\ v_0 =0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 1\ cm\\ \sin \varphi = 0 \end{array} \right. \Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x = 4\cos(20\pi t) \ (cm)\)

Chọn đápán B.
Giả sử x = A cos ω t + φ
Thời gian giữa hai lần liên tiếp vật qua vị trí cân bằng là nửa chu kỳ nên
T = 2.0 , 5 = 1 s ⇒ ω = 2 π r a d / s
Quãng đường đi được trong 2s (2 chu kì) là: S = 2.4 A = 32 ⇒ A = 4 c m
Tại thời điểm t = 1 , 5 s vật qua vị trí có li độ x = 2 3 cm theo chiều dương
⇒ 2 3 = 4 cos 3 π + φ − 2 π .4 sin 3 π + φ > 0 ⇒ cos φ = − 3 2 sin φ > 0
Suy ra, có thể lấy φ = − 7 π 6

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ \(\omega = \frac{2\pi}{T} = \frac{2\pi}{2} = \pi\) (rad/s)
+ Nhận xét: Trong 2s = 1T, vật đi quãng đường 4.A = 40 cm, \(\Rightarrow\) A=10cm.
+ t = 0, vật qua VTCB theo chiều dương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ \\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình: \(x = 10cos(\pi t -\frac{\pi}{2})\) (cm)