Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

một vật dao động điều hòa dọc theo trục Ox với phương trình: x=3cos(4pi t - pi/3) cm. Quãng đường vật đi được từ thời điểm t1=0 đến thời điểm t2=2/3 là bao nhiêu?
Chu kì: \(T=\frac{2\pi}{4\pi}=0,5s\)
\(t_2-t_1=\frac{10}{6}=\frac{9}{6}+\frac{1}{6}=3T+\frac{T}{3}\)
+ Trong thời gian 3T quảng đường vật đi được là: \(3\cdot4A=12A=12\cdot3=36cm\)
+ Li độ của vật ở thời điểm t1 là: \(x_1=3\cos\left(4\pi\cdot\frac{13}{6}-\frac{\pi}{3}\right)=1,5cm\)
Vận tốc là: \(v_1=-3\cdot4\pi\sin\left(4\pi\cdot\frac{13}{6}-\frac{\pi}{3}\right)=-6\sqrt{3\pi}\left(\frac{cm}{s}\right)\)
Như vậy, lúc này đang có li độ 1,5cm chuyển động theo chiều âm và \(\frac{1}{3}\) chu kì nữa thì vật về đến biên độ âm.
Quãng đường vật đi thêm được là: \(3+1,5=4,5cm\)
Tổng quãng đường vật đã đi là: \(36+4,5=40,5cm\)

Đối với những bài tìm quãng đường trong khoảng từ t1 đến t2 thì bạn lấy t2-t1 rồi phân tích chúng ra thành \(\left[{}\begin{matrix}t_2-t_1=n.\dfrac{T}{2}+t'\\t_2-t_1=n.T+t''\end{matrix}\right.\) để dễ dàng tính. Tuyệt đối ko được phân tích thành T/4 hay T/3; T/6;T/v.v. bởi nó ko luôn đúng trong các trường hợp, nếu bạn cần mình sẽ lấy ví dụ cụ thể. Giờ mình sẽ áp dụng vô bài của bạn
\(t_2-t_1=\dfrac{17}{3}-2=\dfrac{11}{3}\left(s\right)=3+\dfrac{2}{3}\)
\(T=\dfrac{2\pi}{\pi}=2s\Rightarrow t_2-t_1=3.\dfrac{T}{2}+\dfrac{2}{3}\)
Trong 3T/2 vật đi được quãng đường là: \(S_1=6A=30\left(cm\right)\)
Tại thời điểm t1=2s, lúc này vật đã quay được:\(\varphi=2\pi\left(rad\right)\) nghĩa là quay về vị trí ban đầu
Trong 2/3 s vật quay được góc: \(\varphi=\dfrac{2}{3}\pi\left(rad\right)\)
Sử dụng đường tròn lượng giác, vật ở vị trí có pha là 2pi/3, quay được góc 2pi/3 thì lúc này vật có li độ là: \(x=-2,5\left(cm\right)\)
Nghĩa là vật đi từ vị trí có li độ x1=-2,5 theo chiều âm đến vị trí có li độ x2=-2,5 theo chiều dương, vậy quãng đường vật đi được là: \(S_2=\dfrac{A}{2}+\dfrac{A}{2}=A=5\left(cm\right)\)
Vậy tổng quãng đường vật đi được là: \(S=S_1+S_2=35\left(cm\right)\)

Ta có: \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Quãng đường mà vật đi được: \(\Delta t=t_2-t_1=\dfrac{11}{12}=0,5+\dfrac{0,5}{2}+\dfrac{1}{6}\)
\(=T+\dfrac{T}{2}+\dfrac{1}{6}\) \(\Rightarrow S=4A+2A+\Delta S\) (\(\Delta S\) là quãng đường mà vật đi được trong khoảng thời gian 1/6 giây ).
Thời điểm ban đầu, góc là pi/3 tức -60 độ.
t1 = 13/6 = 4T + T/3 Ứng với 4 vòng quay và 1 góc 360/3 = 120 độ.
Khoảng thời gian giữa t1 và t2 là t2 - t1 = 11/12s = T + 5/6T Ứng với 1 vòng quay + 1 góc 360*5/6 = 300 độ.
Biểu diễn lên đường tròn.
Quãng đường đi từ t1 đến t2 sẽ là 4A (đi hết 1 vòng) + quãng đường anh tô đỏ (khi quay 1 góc 300 độ)
Tổng quãng đường: S=4A+A.cos60+3A.=45

Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Chu kỳ dao động T = 2s
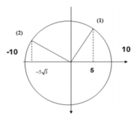
Quan sát trên hình vẽ ta thấy quãng đường vật đi được từ thời điểm t1 = 0,5s ứng với vị trí (1) đến thời điểm t2 = 1s ứng với vị trí (2) là: (5 + 5 3 ) = 13,7cm
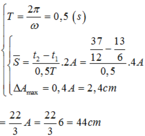



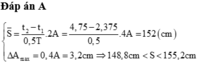

Chu kì: \(T=2\pi/4\pi=0,5s\)
\(t_2-t_1=10/6=9/6+1/6=3T+\dfrac{T}{3}\)
+ Trong thời gian 3T quãng đường vật đi được là: \(3.4A=12A=12.3=36cm\)
+ Li độ của vật ở thời điểm t1 là: \(x_1=3\cos(4\pi.\dfrac{13}{6}-\dfrac{\pi}{3})=1,5cm\)
Vận tốc là: \(v_1=-3.4\pi\sin(4\pi.\dfrac{13}{6}-\dfrac{\pi}{3})=-6\sqrt 3\pi(cm/s)\)
Như vậy, lúc này vật đang có li độ 1,5cm chuyển động theo chiều âm và trong 1/3 chu kì nữa thì vật về đến biên độ âm.
Quãng đường vật đi thêm được là: \(3+1,5=4,5cm\)
Tổng quãng đường vật đã đi là: \(36+4,5=40,5cm\)
Bài này không dùng đường tròn thì giải bằng niềm tin à bạn