Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

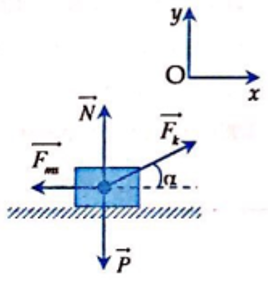
Theo định luật ll Niu tơn:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{F_k}=m\cdot\overrightarrow{a}\)
\(Oy:N-P-F_k\cdot sin\alpha=0\) \(\Rightarrow N=P-F_k\cdot sin\alpha=m\cdot g-F_ksin\alpha=2\cdot10-F_k\cdot sin30\)
\(\Rightarrow F_{ms}=\mu\cdot N=0,1\cdot\left(20-\dfrac{1}{2}F_k\right)\)
\(Ox:F_k\cdot cos\alpha-F_{ms}=m\cdot a\)
\(\Rightarrow F_k\cdot cos30-F_{ms}=2\cdot a\)
\(\Rightarrow a=???\)
Vì đề bài ko cho \(F\) bằng bao nhiêu nên mình ko thay số đc nhé

a. Ta có công của lực F:
A F = F . s . cos 45 0 = 10.2. 2 2 = 14 , 14 ( J ) > 0
Công dương vì là công phát động
Công của lực ma sát
A F m s = F m s . s . cos 180 0 = − μ . N . s = − μ ( P − F sin 45 0 ) . s A F m s = − 0 , 2. ( 2.10 − 10. 2 2 ) .2 = − 5 , 17 < 0
Công âm vì là công cản
b. Hiệu suất H = A c i A t p .100 %
Công có ích
A c i = A F − | A F m s | = 14 , 14 − 5 , 17 = 8 , 97 ( J )
Công toàn phần
A t p = A F = 14 , 14 ( J ) ⇒ H = 8 , 97 14 , 14 .100 % = 63 , 44 %

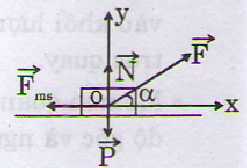
Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


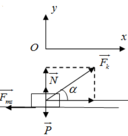
a. Chọn hệ quy chiếu như hình vẽ vật chịu tác dụng của các lực: N → , P → , F m s → , F →
Theo định lụât II Newton ta có: N → + P → + F m s → + F → = m a →
Chiếu lên trục Ox: F . c os α − F m s = m a 1
Chiếu lên trục Oy:
N − P + F . sin α = 0 ⇒ N = P − F . sin α 2
Từ (1) và (2)
⇒ F . c os α − μ . ( P − F . sin α ) = m a I
⇒ a = 2. 2 . cos 45 0 − 0 , 2 1.10 − 2 2 . sin 45 0 1 = 0 , 4 m / s 2
Quãng đường vật chuyển động sau 10s là:
s = v 0 t + 1 2 a t 2 = 0.10 + 1 2 .0.4.10 2 = 20 m
b. Để vật chuyển động thẳng đều thì a = 0 m / s 2
Từ ( I ) ta có ⇒ F . c os α − μ . ( P − F . sin α ) = 0
⇒ μ = F cos 45 0 P − F sin 45 0 = 2 2 . 2 2 1.10 − 2 2 . 2 2 = 0 , 25

F F N P N O y x ms
a)\(\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
chiếu lên trục Ox đã chọn
cos\(\alpha\).F-Fms=m.a
\(\Leftrightarrow cos\alpha.F-\mu.N=m.a\) (1)
chiếu lên trục Oy đã chọn
P=N+sin\(\alpha.F\Rightarrow N=P-sin\alpha.F\) (2)
từ (1),(2)\(\Rightarrow\)a=0,4m/s2
sau 10s quãng đường đi được là
s=v0.t+a.t2.0,5=20m
b)để vật chuyển động đều (a=0)
\(\Rightarrow\)F-Fms=0\(\Rightarrow F=\mu.N\)\(\Rightarrow\)\(\mu\)=\(\dfrac{\sqrt{2}}{4}\)

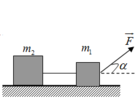
Phân tích các lực tác dụng lên hệ vật
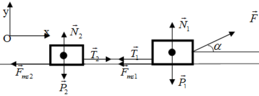
Chọn hệ quy chiếu như hình vẽ như hình vẽ, chiều dương (+) là chiều chuyển động
Xét vật 1 : Áp dụng định luật II Newton ta có
F → + F → m s 1 + N → + P → + T → 1 = m 1 a →
Chiếu lên Ox: F cos α − F m s 1 − T 1 = m 1 a
Chiếu lên Oy: N 1 − P 1 + F sin α = 0 ⇒ N 1 = m 1 g − F sin α
Thay vào (1) ta được:
F cos α − μ m 1 g − F sin α − T 1 = m 1 a
Tương tự đối với vật 2: F → m s 2 + N → 2 + P → 2 + T → 2 = m 2 a →
Chiếu lên Ox: − F m s 2 + T 2 = m 2 a
Chiếu lên Oy: N 2 = P 2 = m 2 g
Thay vào (2) ta được − μ m 2 g + T 2 = m 2 a
Vì dây không dãn nên T = T 1 = T 2
F cos α − μ m 1 g − F sin α − T 1 = m 1 a − μ m 2 g + T 2 = m 2 a
Cộng vế ta có :
F cos α − μ m 1 g − F sin α − μ m 2 g = ( m 1 + m 2 ) a
⇒ a = F cos α − μ ( m 1 g − F sin α ) − μ m 2 g ( m 1 + m 2 )
⇒ a = 10. cos 30 0 − 0 , 1 3.10 − 10. sin 30 0 − 0 , 1.2.10 3 + 2 = 0 , 832 m / s 2
Thay vào (**) ta có
T = m 2 a + μ m 2 g = 2.0 , 832 + 0 , 1.2.10 = 3 , 664 N

chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F

Fms=\(\mu\).N
N=\(P-sin\alpha.F=\)\(20-10\sqrt{2}\)N
\(\Rightarrow F_{ms}=\)\(4-2\sqrt{2}\)N
công của lực ma sát
\(A_{F_{ms}}=F_{ms}.s.cos180^0\)=\(-8+4\sqrt{2}\)J