Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc tức thời của chuyển động tại \(t = 2\) là:
\(\begin{array}{l}v\left( 2 \right) = s'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{s\left( t \right) - s\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{\left( {4{t^3} + 6t + 2} \right) - \left( {{{4.2}^3} + 6.2 + 2} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t + 2 - 46}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t - 44}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{2\left( {t - 2} \right)\left( {2{t^2} + 4t + 11} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} 2\left( {2{t^2} + 4t + 11} \right) = 2\left( {{{2.2}^2} + 4.2 + 11} \right) = 54\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = 54\left( {m/s} \right)\)

a) Vận tốc tức thời \(v\left( t \right)\) tại thời điểm \(t\) là: \(v\left( t \right) = s'\left( t \right) = 6{t^2} + 4\).
b) Gia tốc \(a\left( t \right)\) của chuyển động tại thời điểm \(t\) là: \(a\left( t \right) = v'\left( t \right) = 12t\).
Gia tốc của chuyển động tại thời điểm \(t = 2\) là: \(a\left( 2 \right) = 12.2 = 24\).

Vận tốc: v(t) = S’(t) = (t3 – 3t2 – 9t)' = 3t2 – 6t – 9.
Gia tốc : a(t) = v’(t) = (3t2 – 6t – 9)’ = 6t – 6.
a) Khi t = 2s, v(2) = 3.22 – 6.2 – 9 = -9 (m/s).
b) Khi t = 3s, a(3) = 6.3 – 6 = 12 (m/s2).
c) v(t) = 0 ⇔ 3t2 – 6t – 9 = 0 ⇔ t = 3 (vì t > 0).
Khi đó a(3) = 12 m/s2.
d) a(t) = 0 ⇔ 6t – 6 = 0 ⇔ t = 1.
Khi đó v(1) = 3.12 – 6.1 – 9 = -12 (m/s).

a)
\(\begin{array}{l}\begin{array}{*{20}{l}}{\left[ {5;5,1} \right]}\end{array}:t = 5,1 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{1^2} - 4,{{9.5}^2}}}{{5,1 - 5}} = 49,49\\\begin{array}{*{20}{l}}{\left[ {5;5,05} \right]}\end{array}:t = 5,05 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{05}^2} - 4,{{9.5}^2}}}{{5,05 - 5}} = 49,245\\\begin{array}{*{20}{l}}{\left[ {5;5,01} \right]}\end{array}:t = 5,01 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{01}^2} - 4,{{9.5}^2}}}{{5,01 - 5}} = 49,049\\\begin{array}{*{20}{l}}{\left[ {5;5,001} \right]}\end{array}:t = 5,001 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{001}^2} - 4,{{9.5}^2}}}{{5,001 - 5}} = 49,0049\\\begin{array}{*{20}{l}}{\left[ {4,999;5} \right]}\end{array}:t = 4,999 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{999}^2} - 4,{{9.5}^2}}}{{4,999 - 5}} = 48,9951\\\begin{array}{*{20}{l}}{\left[ {4,99;5} \right]}\end{array}:t = 4,99 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{99}^2} - 4,{{9.5}^2}}}{{4,99 - 5}} = 48,951\end{array}\)

Ta thấy: \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) càng gần 49 khi \(t\) càng gần 5.
b)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,{{9.5}^2}}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - {5^2}} \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - 5} \right)\left( {t + 5} \right)}}{{t - 5}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + 5} \right) = 4,9\left( {5 + 5} \right) = 49\end{array}\)
c)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,9.t_0^2}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - t_0^2} \right)}}{{t - t_0^2}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + {t_0}} \right) = 4,9\left( {{t_0} + {t_0}} \right) = 9,8{t_0}\end{array}\)

Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s

Chọn D.
Gia tốc chuyển động tại t = 3s là s”(3)
Ta có: s’(t) = 54 và s’’(t) = 0
Vậy vật chuyển động với gia tốc là 0 nên tại t = 3 thì a = 0.

- Gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.
- Ta có:
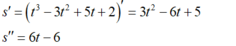
- Suy ra, phương trình gia tốc của chuyển động là:
a(t) = s’’(t) = 6t – 6 ( m / s 2 )
- Do đó, gia tốc của chuyển động khi t = 3 là: a(3) = 12 ( m / s 2 )
Chọn D.

Đáp án D
Ta có gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.
s ' = t 3 - 3 t 2 + 5 t + 2 ' = 3 t 2 - 6 t + 5
s ' ' = 6 t - 6 ⇒ s ' ' 3 = 12

$[v(t) = \frac{ds(t)}{dt} = \frac{d}{dt}(2t^3+4t+1)]$
$[a(t) = \frac{dv(t)}{dt} = \frac{d}{dt}(6t^2 + 4)]$
$[a(t) = 12t]$
Khi (t = 1), ta có:
$[v(1) = 6(1)^2 + 4 = 10 , \text{m/s}]$4
$[a(1) = 12(1) = 12 , \text{m/s}^2]$
Vậy, khi (t = 1), vận tốc của vật là 10 m/s và gia tốc của vật là $12 m/s$