Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Gọi vận tốc của vận động viên chạy và vận động viên đua xe đạp là: v1, v2 (v1> v2> 0). Khoảng cách giữa hai vận động viên chạy và hai vận động viên đua xe đạp là l1, l2 (l2>l1>0). Vì vận động viên chạy và vận động viên đua xe đạp chuyển động cùng chiều nên vận tốc của vận động viê đua xe khi chộn vận động viên chạy làm mốc là:
v21= v2 - v1 = 10 - 6 = 4 (m/s).
- Thời gian hai vận động viên đua xe vượt qua một vận động viên chạy là:
\(t_1=\frac{l_2}{v_{21}}=\frac{20}{4}=5\)(s)
- Thời gian một vận động viên đua xe đạp đang ở ngang hàng một vận động viên chạy đuổi kịp một vận động viên chạy tiếp theo là:
\(t_1=\frac{l_2}{v_{21}}=\frac{10}{4}=2,5\) (s)

1/
Gọi S là độ dài quãng đường AB, gọi t là thời gian chuyển động hết 2/3 quãng đường cuối.Ta có :
\(\dfrac{2}{3}S=v_2.\dfrac{2}{3}t+v_3.\dfrac{1}{3}t\Rightarrow t=\dfrac{2S}{2.v_2+v_3}=\dfrac{2S}{2.45+30}=\dfrac{S}{60}\left(h\right)\)
Mặt khác : \(\dfrac{S}{v}=\dfrac{S}{3v_1}+t\Rightarrow\dfrac{S}{v}=\dfrac{S}{3v_1}+\dfrac{S}{60}\Rightarrow v=40km/h\)
2/gọi t (h) là tổng thời gian xe đi hết quãng đường AB, gọi S là độ dài quãng đường xe đi trong 3/5 tổng thời gian cuối.
Ta có : \(\dfrac{\dfrac{3}{4}S}{v_2}+\dfrac{\dfrac{1}{4}S}{v_3}=\dfrac{3}{5}t\).Thay số => S = 14,4t (km)
Mặt khác: \(v.t=\dfrac{2}{5}t.v_1+S\Rightarrow v.t=\dfrac{2}{5}v_1.t+14,4t\Rightarrow v=30,4km/h\)

+) Nửa quãng đường đầu : \(200=v_1\cdot t_1\)
Nửa quãng đường sau : \(200=v_2\cdot t_2\)
=> Ta có phương trình \(v_1\cdot t_1=v_2\cdot t_2\Leftrightarrow v_1\cdot t_1=\dfrac{v_1}{2}\cdot t_2\left(1\right)\)
+) Theo đề ta có \(t_1+t_2=60s\)(2)
(1) , (2) => Ta có hpt :
\(\left\{{}\begin{matrix}v_1\cdot t_1=\dfrac{v_1}{2}\cdot t_2\\t_1+t_2=60\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2=\dfrac{t_2}{t_1}\\t_1+t_2=60\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=20s\\t_2=40s\end{matrix}\right.\)
Vận tốc : \(\left\{{}\begin{matrix}v_1=\dfrac{200}{20}=10\left(m/s\right)\\v_2=\dfrac{200}{40}=5\left(m/s\right)\end{matrix}\right.\)

Vận tốc trung bình của vận động viên trong mỗi khoảng thời gian là:
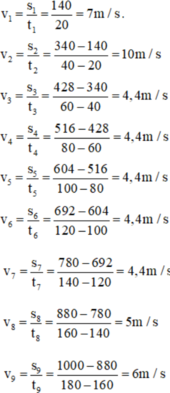
Dựa vào kết quả trên, ta thấy:
Trong hai quãng đường đầu: vận động viên chuyển động nhanh dần.
Trong năm quãng đường sau: vận động viên chuyển động đều.
Hai quãng đường sau cùng: vận động viên chuyển động nhanh dần.

a)ta có:
thời gian ô tô đi trên quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}\)
thời gian ô tô đi trên đoạn đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của ô tô trên toàn bộ quãng đường là:
\(v_{tb1}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2v_1}+\frac{S}{2v_2}}=\frac{S}{S\left(\frac{1}{2v_1}+\frac{1}{2v_2}\right)}\)
\(\Leftrightarrow v_{tb1}=\frac{1}{\frac{1}{2v_1}+\frac{1}{2v_2}}=\frac{1}{\frac{v_2+v_1}{2v_1v_2}}=\frac{2v_1v_2}{v_1+v_2}\)
b)ta có:
quãng đường ô tô đi được trong nửa thời gian đầu là:
S1=v1t1=\(\frac{v_1t}{2}\)
quãng đường ô tô đi được trong thời gian còn lại là:
S2=v2t2=\(\frac{v_2t}{2}\)
vận tốc trung bình của ô tô là:
\(v_{tb2}=\frac{S_1+S_2}{t}=\frac{\frac{vt_1}{2}+\frac{v_2t}{2}}{t}\)
\(\Leftrightarrow v_{tb2}=\frac{t\left(\frac{v_1}{2}+\frac{v_2}{2}\right)}{t}=\frac{v_1+v_2}{2}\)
c)lấy vtb1-vtb2 ta có:
\(\frac{2v_1v_2}{v_1+v_2}-\frac{v_1+v_2}{2}=\frac{4v_1v_2-\left(v_1+v_2\right)^2}{2v_1+2v_2}\)
\(=\frac{4v_1v_2-\left(v_1^2+2v_1v_2+v_2^2\right)}{2v_1+2v_2}\)
\(=\frac{-v_1^2+2v_1v_2-v_2^2}{2v_1+2v_2}\)
\(=\frac{-\left(v_1-v_2\right)^2}{2v_1+2v_2}\)
mà (v1-v2)2\(\ge\) 0 nên -(v1-v2)2\(\le\) 0
mà vận tốc ko âm nên 2v1+2v2>0
từ hai điều trên nên ta suy ra vận tốc trung bình tìm được ở câu a) bé hơn câu b)

Bài 3 :
Gọi quãng đường AB là : s
Ta có pt : \(v_{tb}=\dfrac{s}{t_1+t_2}\)
\(\Leftrightarrow48=\dfrac{s}{\dfrac{s}{40}+\dfrac{s}{v}}\)
\(\Leftrightarrow48=s\left(\dfrac{1}{\dfrac{1}{4}+\dfrac{1}{v}}\right)\)
\(\Leftrightarrow\) \(\dfrac{48}{s}=\dfrac{1}{\dfrac{1}{4}+\dfrac{1}{v}}\)
\(\Leftrightarrow s=48.\dfrac{1}{4}+\dfrac{1}{v}\)
\(\Leftrightarrow s=12+\dfrac{1}{v}\)
Bài 1:
Gọi S là độ dài quãng đường AB. Ta có \(t_1=\dfrac{S}{4v_1}\) ,\(t_2=\dfrac{3S}{8v_2}\).
Gọi \(t_3\) là thời gian cuối ta có : \(\dfrac{1}{2}t_3.v_1+\dfrac{1}{2}t_3v_2=\dfrac{3}{8}S\Rightarrow t_3=\dfrac{3S}{4\left(v_1+v_2\right)}\) Ta có: \(\dfrac{S}{v}=t_1+t_2+t_3\Rightarrow v_{tb}=\dfrac{8v_1.v_2\left(v_1+v_2\right)}{3v_1^2+2v_2^2+11v_1.v_2}\)
Thời gian xe ô tô chuyển động trên nửa đoạn đường đầu là :
\(t_1=\frac{s}{2.40}=\frac{s}{80}\left(h\right)\)
Nửa đoạn đường sau :
* Nửa thời gian đầu xe đi được quãng đường:
\(s_1=v_1t_1=\frac{37.t}{2}\left(km\right)\)
* Nửa thời gian sau xe đi được quãng đường:
\(s_2=\frac{43t}{2}\left(km\right)\)
Vận tốc trung bình của xe trong nửa đoạn đường sau là:
\(v'_{tb}=\frac{s_1+s_2}{t_1+t_2}=\frac{\frac{37t}{2}+\frac{43t}{2}}{t}=40\left(km/h\right)\)
vận tốc trung bình trên cả đoạn đường AB là:
\(v_{tb}=\frac{s}{\frac{s}{80}+\frac{s}{40}}=\frac{s}{s\left(\frac{1}{80}+\frac{1}{40}\right)}=\frac{80}{3}\left(km/h\right)\)


không để nguồn à bạn?