Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mỗi cách sắp xếp 5 bạn học sinh vào 5 chiếc ghế là một hoán vị của 5 bạn học sinh. Do đó, số cách sắp xếp 5 bạn học sinh ngồi vào 5 cái ghế là hoán vị là:
\({P_5} = 5!\) (cách)
b) Khi bạn Nga nhất định ngồi vào chiếc ghế ngoài cùng bên trái, thì số cách sắp xếp là số cách sắp xếp 4 bạn còn lại vào 4 chiếc ghế, mỗi cách như vậy là một hoán vị của 4 bạn học sinh. Do đó, số cách sắp xếp là:
\({P_4} = 4! = 24\) (cách)

a: SỐ cách xếp là;
5!*6!*2=172800(cách)
b: Số cách xếp là \(6!\cdot5!=86400\left(cách\right)\)

a, Số cách sắp xếp 20 bạn để ngồi vào hàng đầu tiên là: \(A_{60}^{20}\) (cách)
b, Sau khi sắp xếp xong hàng đầu tiên, số cách sắp xếp 20 bạn để ngồi vào hàng thứ hai là: \(A_{40}^{20}\) (cách)
c, Sau khi sắp xếp xong hai hàng đầu, số cách sắp xếp 20 bạn để ngồi vào hàng thứ ba là: \({P_{20}} = 20!\) (cách)

a) Số cách chọn 1 bạn từ nhóm 15 bạn là tổ hợp chập 1 của 15 \(C_{15}^1 = 15\) cách
b) Việc chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau gồm 3 công đoạn:
Công đoạn 1: Chọn 1 bạn từ lớp 10A có 4 cách
Công đoạn 2: Chọn 1 bạn từ lớp 10B có 5 cách
Công đoạn 3: Chọn 1 bạn từ lớp 10C có 6 cách
Áp dụng quy tắc nhân, ta có \(4.5.6 = 120\) cách chọn 3 thành viên của nhóm đang học ở ba lớp khác nhau
c) Việc chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau có 3 trường hợp:
TH1: 2 bạn đang học ở lớp 10A và 10B có \(4.5 = 20\) cách
TH2: 2 bạn đang học ở lớp 10A và 10C có \(4.6 = 24\) cách
TH3: 2 bạn đang học ở lớp 10C và 10B có \(6.5 = 30\) cách
Áp dụng quy tắc cộng, ta có \(20 + 24 + 30 = 74\) cách chọn 2 thành viên của nhóm đang học ở hai lớp khác nhau

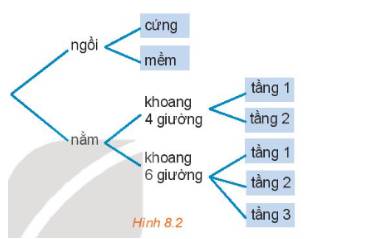
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2 + 3 = 5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2 + 5 = 7 (loại vé)

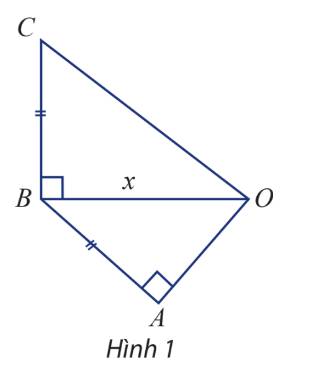
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)

a, Có 3 cách để chọn nhóm trình bày thứ nhất.
b, Sau khi đã chọn nhóm trình bày thứ nhất thì còn lại 2 nhóm, vì vậy có 2 cách để chọn nhóm trình bày thứ 2.
c, Sau khi đã chọn nhóm trình bày thứ nhất và thứ hai thì còn lại một nhóm duy nhất nên ta có 1 cách chọn nhóm trình bày thứ 3.
d, Áp dụng quy tắc nhân, số hoán vị được tạo ra là: 3.2.1 = 6 (hoán vị).

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)



Mỗi cách sắp xếp 6 bạn vào 6 chiếc ghế trống là hoán vị của 6 chiếc ghế. Do đó, số cách sắp xếp chỗ ngồi cho các thành viên trong nhóm là
\({P_6} = 6! = 720\) (cách)