Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi l1 là chiều dài cánh tay đòn 1 ( ở đây là OA) l2 là chiều dài cánh tay đòn 2 ( ở đây là OB)
l1+l2=150 cm =1,5 m (1)
m1=3kg => P1=30(N)
m2=6kg => P2=60(N)
Để hệ thống cân bằng thì:
m1.l1=m2.l2
=> 30l1=60l2 => l1 - 2l2= 0 ( đơn giản mỗi vế cho 30) (2)
Từ (1) và (2) ta có hệ phương trình
l1+l2=1,5
l1 - 2l2=0
=> l1=1 (m)
l2=0,5(m)

Bài 1.
a)\(OA=40cm\Rightarrow OB=160-40=120cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1\cdot l_1=F_2\cdot l_2\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{l_2}{l_1}=\dfrac{OB}{OA}=\dfrac{120}{40}=3\)
\(\Rightarrow F_2=\dfrac{F_1}{3}=\dfrac{P_1}{3}=\dfrac{10m_1}{3}=\dfrac{10\cdot9}{3}=30N\)
\(\Rightarrow m_2=\dfrac{P_2}{10}=\dfrac{F_2}{10}=\dfrac{30}{10}=3kg\)
b)Vật \(m_2\) giữ nguyên không đổi. \(\Rightarrow F_2=P_2=30N\)
\(OB'=60cm\Rightarrow OA'=160-60=100cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1'\cdot l_1'=F_2\cdot l_2'\)
\(\Rightarrow F_1'=\dfrac{F_2\cdot l_2'}{l_1'}=\dfrac{30\cdot60}{100}=18N\) \(\Rightarrow m_1'=1,8kg\)
Mà \(m_1=9kg\)
\(\Rightarrow\) Phải giảm vật đi một lượng là:
\(\Delta m=m_1-m_1'=9-1,8=7,2kg\)
Bài 2.
a)Áp dụng hệ cân bằng của đòn bẩy:
\(\dfrac{F_1}{F_2}=\dfrac{OA}{OB}=\dfrac{10m_1}{10m_2}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\Rightarrow2OA=3OB\left(1\right)\)
Mà \(OA+OB=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=72cm\\OB=48cm\end{matrix}\right.\)
Vậy O nằm cách A và B lần lượt một đoạn là 72cm và 48cm.
b)Giữ nguyên vật 2 \(\Rightarrow F_2=P_2=10m_2=40N\)
Tăng khối lượng \(m_1\) lên 2kg thì \(F_1=P_1=10\cdot\left(2+6\right)=80N\)
Để thanh AB nằm cân bằng:
\(F_1\cdot OA'=F_2\cdot OB'\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{OB'}{OA'}=\dfrac{80}{40}=2\)
\(\Rightarrow OB'=2OA'\left(1\right)\)
Mà \(OA'+OB'=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA'=40cm\\OB'=80cm\end{matrix}\right.\)
Vậy O nằm trên AB cách A và B lần lượt là 40cm và 80 cm.

Để thanh AB nằm ngang quả cầu A có khối lượng là \(1.5kg\)

Đáp án C
- Vì thanh nhẹ có thể quay quanh điểm O nên ta coi O là điểm tựa của đòn bẩy.
- Để hệ thống cân bằng ta có điều kiện cân bằng đòn bẩy như sau:
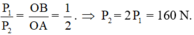
- Khối lượng vậy treo vào đầu B là:
160 : 10 = 16 (kg)
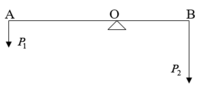

Khi hai vật treo ngoài không khí ta có cân bằng lực:
\(P_1\cdot l_1=P_2\cdot l_2\Rightarrow l_1=l_2=\dfrac{l}{2}=\dfrac{80}{2}=40\left(cm\right)\)
Nhúng cả hai quả cầu ngập trong nước ta có:
\(\left(P_1-F_{A_1}\right)\cdot l_1'=\left(P_2-F_{A_2}\right)\cdot l_2'\)
Trong đó: \(\left\{{}\begin{matrix}l_1'=l_1+6x\left(cm\right)\\l_2'=l_2-6x\left(cm\right)\end{matrix}\right.\) và \(\left\{{}\begin{matrix}F_{A_1}=V_1\cdot d_0=\dfrac{P_1}{d_1}\cdot d_0\\F_{A_2}=V_2\cdot d_0=\dfrac{P_2}{d_2}\cdot d_0\end{matrix}\right.\)
Khi đó: \(\left(P_1-\dfrac{P_1}{d_1}\cdot d_0\right)\left(l_1+6x\right)=\left(P_2-\dfrac{P_2}{d_2}\cdot d_0\right)\left(l_2-6x\right)\)
\(\Rightarrow P_1\cdot l_1+P_1\cdot6x-\dfrac{P_1}{d_1}\cdot d_0\cdot l_1-\dfrac{P_1}{d_1}\cdot d_0\cdot6x=P_2\cdot l_2-P_2\cdot6x-\dfrac{P_2}{d_2}\cdot d_0\cdot l_2+\dfrac{P_2}{d_2}\cdot d_0\cdot6x\)
Mà \(\left\{{}\begin{matrix}P_1=P_2\\l_1=l_2=40cm=0,4m\end{matrix}\right.\)
Khi đó: \(6x-\dfrac{d_0\cdot l_1}{d_1}-\dfrac{6x\cdot d_0}{d_1}=-6x-\dfrac{d_0\cdot l_2}{d_2}+\dfrac{6x\cdot d_0}{d_2}\)
\(\Rightarrow6x-\dfrac{10^4\cdot0,4}{3\cdot10^4}-\dfrac{6x\cdot10^4}{3\cdot10^4}=-6x-\dfrac{10^4\cdot0,4}{3,9\cdot10^4}+\dfrac{6x\cdot10^4}{3,9\cdot10^4}\)
\(\Rightarrow x=\dfrac{1}{275}\left(m\right)\approx0,36\left(cm\right)\)

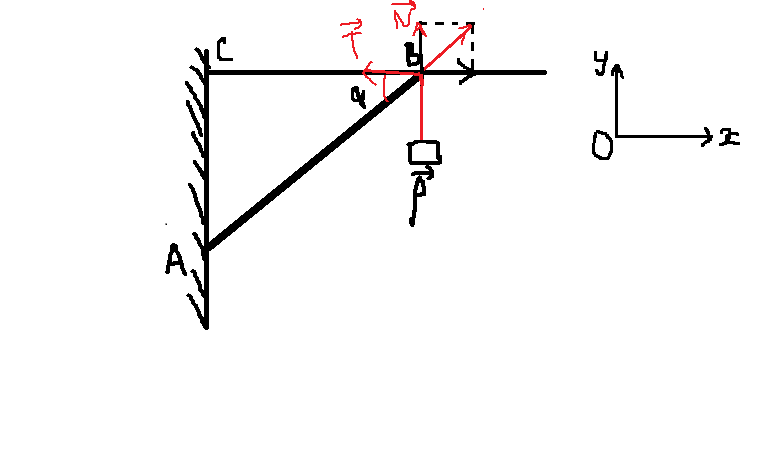
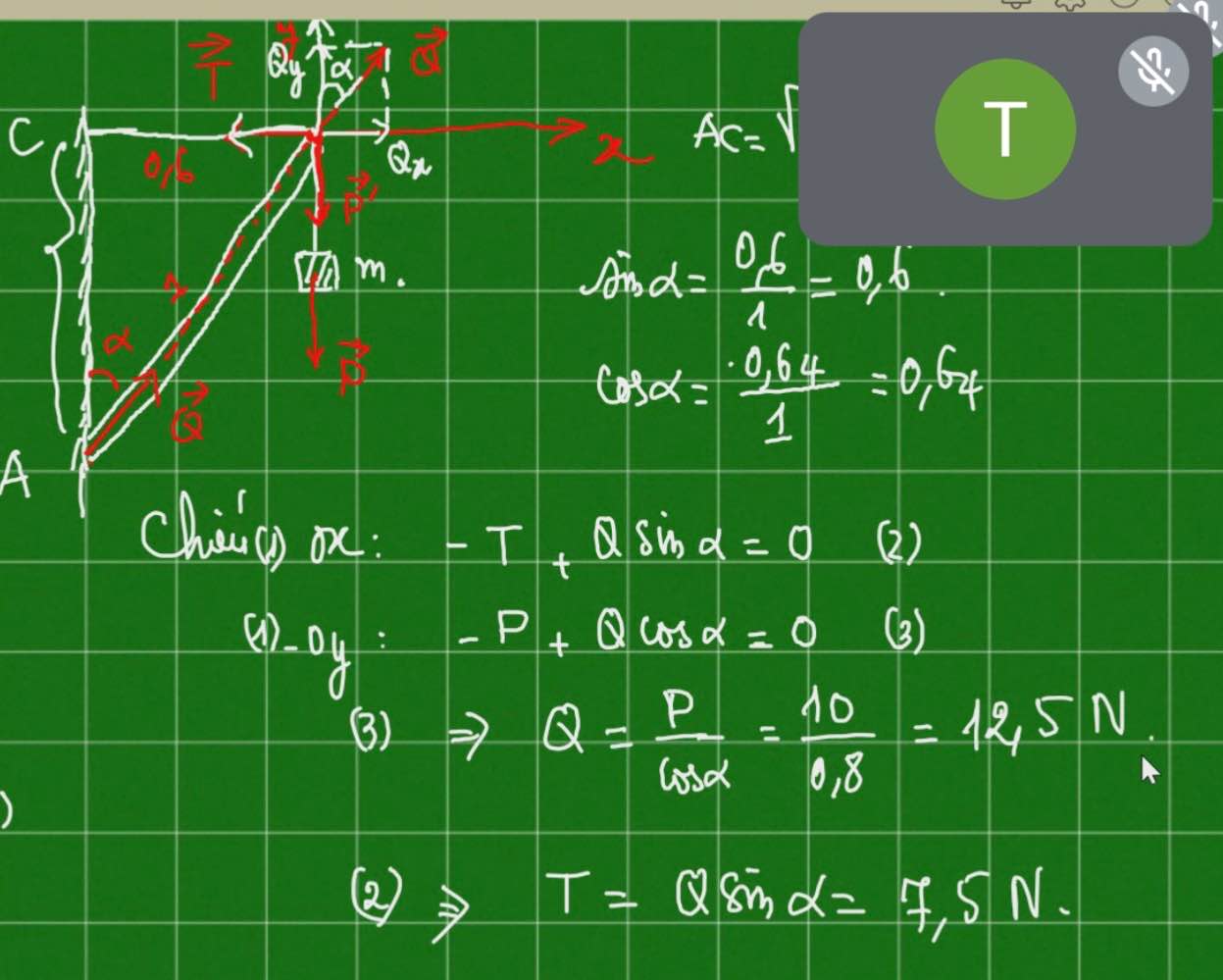
Các lực tác dụng lên thanh AB.
+Trọng lực \(\overrightarrow{P}\) hướng xuống.
+Lực căng dây \(\overrightarrow{T}\).
+Phản lực \(\overrightarrow{N}\).
Tổng hợp lực: \(\overrightarrow{P}+\overrightarrow{T}+\overrightarrow{N}=\overrightarrow{0}\) \(\left(1\right)\)
Chiếu (1) lên trục Oxy ta đc:
Ox: \(Ncosa-T=0\)\(\Rightarrow T=Ncosa\)
Oy: \(Nsina-P=0\)\(\Rightarrow N=\dfrac{P}{sina}\)
\(cosa=\dfrac{BC}{AB}=\dfrac{0,6}{1}=0,6\)
\(sina=\sqrt{1-cos^2a}=\sqrt{1-0,6^2}=0,8\)
\(\Rightarrow N=\dfrac{P}{sina}=\dfrac{10m}{sina}=\dfrac{10\cdot1}{0,8}=12,5N\)
\(T=Ncosa=12,5\cdot0,6=7,5N\)
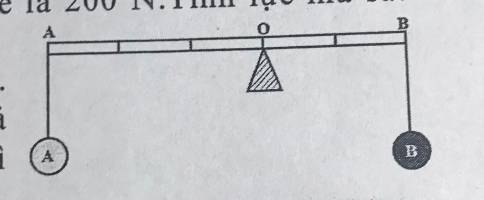
giải
khối lượng của thanh cứng là \(m=\frac{P}{10}=\frac{3}{10}=0,3\left(kg\right)\)
vì OA=OB=\(\frac{1}{2}\) thanh cứng nên:
\(\frac{1}{2}\)của 0,3kg là
\(\frac{3}{20}=0,15kg\)
khối lượng của đoạn OB và vật B là 0,15+0,2=0,35kg
cân thăng bằng. Suy ra ta có: OB+B=OA+A
\(\Rightarrow0,35=0,15+A\)
\(\Rightarrow A=0,35-0,15=0,2kg\)