Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=sv1t1=sv1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=sv2t2=sv2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb=2st1+t2vtb=2st1+t2 (3)
Kết hợp (1); (2); (3) có: 1v1+1v2=2vtb1v1+1v2=2vtb
Thay số vtb = 8km/h; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h
Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=s/v1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=s/v2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb=2s/t1+t2 (3)
Kết hợp (1); (2); (3) có: 1/v1+1/v2=2/vtb
Thay số vtb = 8km/h; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
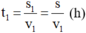
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
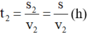
Vậy tổng thời gian đi hết cả quãng đường là: 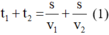
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
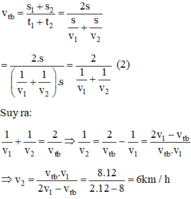

\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}\Rightarrow10=\dfrac{S_{tổng}}{\dfrac{S_{tổng}}{15}+\dfrac{S_{tổng}}{v_2}}=\dfrac{S_{tổng}}{S_{tổng}\left(\dfrac{1}{15}+\dfrac{1}{v_2}\right)}=\dfrac{1}{\dfrac{1}{15}+\dfrac{1}{v_2}}\)
\(\Rightarrow\dfrac{1}{v_2}=\dfrac{1}{10}-\dfrac{1}{15}=\dfrac{1}{30}\Rightarrow v_2=30\left(\dfrac{km}{h}\right)\)

\(=>t1=\dfrac{\dfrac{1}{3}S}{12}=\dfrac{S}{36}\left(h\right)\)
\(=>t2=\dfrac{\dfrac{1}{3}S}{8}=\dfrac{S}{24}\left(h\right)\)
\(=>t3=\dfrac{\dfrac{1}{3}S}{6}=\dfrac{S}{18}\left(h\right)\)
\(=>vtb=\dfrac{S}{t1+t2+t3}=\dfrac{S}{\dfrac{S}{36}+\dfrac{S}{24}+\dfrac{S}{18}}=\dfrac{S}{\dfrac{432S+648S+864S}{15552}}\)
\(=\dfrac{S}{\dfrac{1944S}{15552}}=\dfrac{15552}{1944}=8km/h\)

\(=>vtb=\dfrac{S}{\dfrac{\dfrac{1}{2}S}{v1}+\dfrac{\dfrac{1}{2}S}{v2}}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{2v2}}=\dfrac{S}{\dfrac{S\left(2v2+40\right)}{80v2}}=\dfrac{80v2}{2v2+40}=15\)
\(=>v2=12km/h\)

Ta có: \(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}\)
\(\Leftrightarrow9=\dfrac{\dfrac{2}{3}s+\dfrac{1}{3}s}{\dfrac{\dfrac{2}{3}s}{12}+\dfrac{\dfrac{1}{3}s}{v_2}}=\dfrac{s}{\dfrac{s}{18}+\dfrac{s}{3v_2}}=\dfrac{s}{\dfrac{s\left(18+3v_2\right)}{54v_2}}=\dfrac{54v_2}{18+3v_2}\)
\(\Leftrightarrow v_2=6\left(\dfrac{m}{s}\right)\)

Gọi S là chiều dài quãng đường ta có :
Thời gian đi hết nửa quãng đường đầu là :\(t_1=\frac{S}{2v_1}\)
Thời gian đ hết nửa quãng đường sau là :
\(t_2=\frac{S}{2v_2}\)
Vận tốc trung bình trên cả quãng đường S là :
\(v_{tb}=\frac{S}{\left(t_1+t_2\right)}\Rightarrow\left(t_1+t_2\right)=\frac{S}{v_{tb}}\)
Từ các điều nói trên : \(\frac{1}{v_1}+\frac{1}{v_2}=\frac{2}{v_{tb}}\)
Thế số vào tính được v2 = 7,5 km/h
ta có:
thời gian người đó đi trong nửa quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{30}\)
thời gian người đó đi trong quãng đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{30}+\frac{S}{2v_2}}=\frac{S}{S\left(\frac{1}{30}+\frac{1}{2v_2}\right)}=\frac{1}{\frac{1}{30}+\frac{1}{2v_2}}\)
\(\Leftrightarrow10=\frac{1}{\frac{v_2+15}{30v_2}}=\frac{30v_2}{v_2+15}\)
giải phương trình trên ta có:
v2=7,5km/h
Ta có: \(v_{tb}=\dfrac{s}{\dfrac{\dfrac{1}{2}s}{v'}+\dfrac{\dfrac{1}{2}s}{v''}}=\dfrac{s}{\dfrac{s}{20}+\dfrac{s}{2v''}}=\dfrac{s}{\dfrac{s\left(2v''+20\right)}{40v''}}=\dfrac{40v''}{2v''+20}=8\)
\(=>v''=\dfrac{20}{3}\left(\dfrac{km}{h}\right)\)