Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xe đạp đi với gia tốc là:
\(a = \frac{F}{m} = \frac{{200}}{{60 + 20}} = 2,5\left( {m/{s^2}} \right)\)
Vận tốc của xe đạp sau 5,00 s là:
\(v = {v_0} + at = 0 + 2,5.5 = 12,5\left( {m/s} \right)\)

Áp dụng định luật II niu tơn, ta được
a) Hợp lực tác dụng lên xe ca: F1 = m1. a = 1250. 2,15 = 2687,5 (N)
b) Hợp lực tác dụng lên xe mooc là: F2 - m2.a = 325. 2,15 = 698,75 (N)

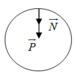
Người diễn viên chịu tác dụng của hai lực P → , N →
Theo định luật II Newton P → + N → = m a →
a. Chiếu theo chiều hướng vào tâm
P + N = m a h t = m . v 2 R ⇒ N = m . v 2 R − P
Muốn không bị rơi thì người đó vẫn ép lên vòng xiếc tức là
N ≥ 0 ⇒ m v 2 R − m g ≥ 0 ⇒ v ≥ g R ⇒ v ≥ 10.10 = 10 ( m / s )
Vậy vận tốc của xe đạp tối thiểu phải là 10m/s.
b. Chiếu theo chiều hướng vào tâm P cos α + N = m v 2 r
⇒ N = m v 2 r − g cos α = 60 10 2 10 − 10. cos 60 0 = 300 N

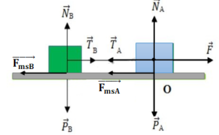
a) Các lực tác dụng lên hệ xe ca và xe moóc được biểu diễn như hình vẽ.
Áp dụng định luật II Niu – Tơn cho xe ca ta có:
![]()
Chiếu lên chiều dương là chiều chuyển động, ta tìm được hợp lực tác dụng lên xe ca là: FhlA = mA. a = 1250. 2,15 = 2687,5 (N)
b) Áp dụng định luật II Niu – Tơn cho xe moóc ta có:
![]()
Chiếu lên chiều dương là chiều chuyển động, ta tìm được hợp lực tác dụng lên xe moóc: FhlB = mB. a = 325. 2,15 = 698,8 (N).

Đáp án D
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực P → và phản lực Q → của vòng xiếc.


Chọn D.

Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực P → và phản lực N → của vòng xiếc
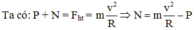
Gọi N ' → là lực ép của người đi xe lên vòng xiếc, ta có:
N’ = N = mv2/R - mg = 80.102/8 – 80.9,8 = 216 N.

Chọn D.
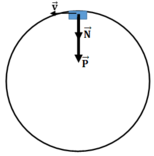
Tại điểm cao nhất của vòng xiếc có các lực tác dụng lên xe là trọng lực và phản lực của vòng xiếc.
Ta có:
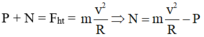
Gọi N ⇀ là lực ép của người đi xe lên vòng xiếc, ta có:
N’ = N = m v 2 /R - mg
= 80. 10 2 /8 – 80.9,8 = 216 N.

Xe đạp đi với gia tốc là:
\(a=\dfrac{F}{m}=\dfrac{200}{60+20}=2,5\left(m/s^2\right)\)
Vận tốc của xe đạp sau 5,00 s là:
\(v=v_0+at=0+2,5.5=12,5\left(m/s\right)\)