Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(I_0=\omega Q_0\Rightarrow \omega = \dfrac{I_0}{Q_0}=10^7\)(rad/s)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{5}{\pi}.10^6\)(hz)
\(\Rightarrow \lambda=\dfrac{c}{f}=\dfrac{3.10^8}{5.10^6}.\pi=188,4m\)
Thời gian để cường độ dòng điện giảm từ cực đại xuống nửa cực đại là T/6, suy ra:
\(\dfrac{T}{6}=\dfrac{8}{3}\Rightarrow T = 16\mu s=16.10^{-6}s\)
Ở thời điểm cường độ trong mạch bằng 0 thì điện tích trong mạch cực đại, suy ra:
\(q=Q_0=\dfrac{I_0}{\omega}=\dfrac{I_0.T}{2\pi}=\dfrac{2,22.16.10^{-6}}{2\pi}=5,65.10^{-6}(C)=5,65 \mu C\)
Sử sụng hệ thức: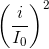 
+
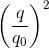= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =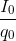 
= 50 (rad/s)
Hướng dẫn giải:
Thời gian để tụ phòng hết điện tích (q0 -> 0) được tính như sau
\(t = \frac{\varphi}{\omega}=\frac{\pi/2}{2\pi/T}=\frac{T}{4} \) => \(T = 4.2.10^{-6}= 8.10^{-6}s.\)
\(I_0 = q_0.\omega = 10^{-8}.\frac{2\pi}{8.10^{-6}}= 2,5.\pi.10^{-3} => I = \frac{I_0}{\sqrt{2}} \approx 5,55 mA.\)
khó không làm nổi
Bài này mình đã từng trả lời rồi, giả thiết phải là UL max= 41U/40, bạn xem lại xem chính xác không nhé.
Ta có giản đồ như sau:
AB biểu diễn điện áp trên điện trở, CD biểu diễn điện áp trên cuộn cảm, BC biểu diễn điện áp giữa 2 đầu tụ điện và AD biểu diễn điện áp trên 2 đầu đoạn mạch.
Ta có thể chọn CD=41, AD=40
Đặt BD=x;BC=41-x( Điều kiện x<41)
\(\Rightarrow AB=\sqrt{40^2-x^2}\)\(\Rightarrow\begin{cases}\tan\varphi_1=\frac{x}{\sqrt{40^2-x^2}}\\\tan\varphi_2=\frac{41-x}{\sqrt{40^2-x^2}}\end{cases}\)
Khi f biến thiên cho Uc max or UL max ta đều có tính chất:
\(\tan\varphi_1\tan\varphi_2=\frac{1}{2}\)\(\Leftrightarrow\frac{x\left(41-x\right)}{1600-x^2}=\frac{1}{2}\Leftrightarrow x=32\)
\(\Rightarrow\cos\varphi_1=\frac{AB}{AD}=0,6\)
\(T = 1/f = 0,001s.\)
\(W_L = \frac{1}{2}W_{Lmax}=> \frac{1}{2}Li^2= \frac{1}{2}\frac{1}{2}LI_0^2.\)
=> \(i= \pm \frac{I_0}{\sqrt{2}}.\)
Thời gian để năng lượng từ trường lại bằng một nửa giá trị cực đại của nó là
I 0 -I 0 I 0 -I 0 2 2
\(\cos \varphi_1 = \frac{I_0/\sqrt{2}}{I_0}= \frac{1}{\sqrt{2}}=> \varphi _1= \frac{\pi}{4}=> \varphi = \frac{\pi}{2}.\)
\(t = \frac{\varphi}{\omega}= \frac{\pi/2}{2\pi/T}= \frac{T}{8}=2,5.10^{-4}s.\)
Khoảng thời gian để \(W_C=W_L\) giữa hai lần liên tiếp là \(\frac{T}{4}s\)
\(=> \frac{T}{4}=10^{-6}s=> T= 4.10^{-6}s.\)
\(W=\frac{1}{2}CU_0^2=> C = 1,25.10^{-7}F. \)
\(T=2\pi \sqrt{LC}=> L = \frac{T^2}{4\pi^2 C}=3,2.10^{-6}H.\)
\(W=\frac{1}{2}LI_0^2=> I_0=0,79A.\)
a. 0,79 A.